14.2. Selection Sort#

Selection sort is a simple sorting algorithm that finds the minimum or maximum element from the unsorted part of the list and swap it with the last element of the unsorted part. It is much less efficient on large lists than more advanced algorithms such as quicksort.

14.2.1. Algorithm#

For sorting in ascending order, the general idea of selection sort is to iterate through the array, and find the maximum element from the unsorted part of the list, which is initially the entire array, then swap it with the last element of the unsorted array. This makes the last element of the array sorted, and the remaining elements of the array unsorted. The process repeats till the entire array gets sorted.

For example, if only the last 3 elements of the array are sorted holding the maximum 3 numbers of the array, we will look at the maximum number in the remaining of the array excluding the last 3 elements. This element will be swapped with the last element from the unsorted array, excluding the last 3 elements. This makes the last 4 elements of the array sorted, and holding the maximum 4 numbers of the entire array.

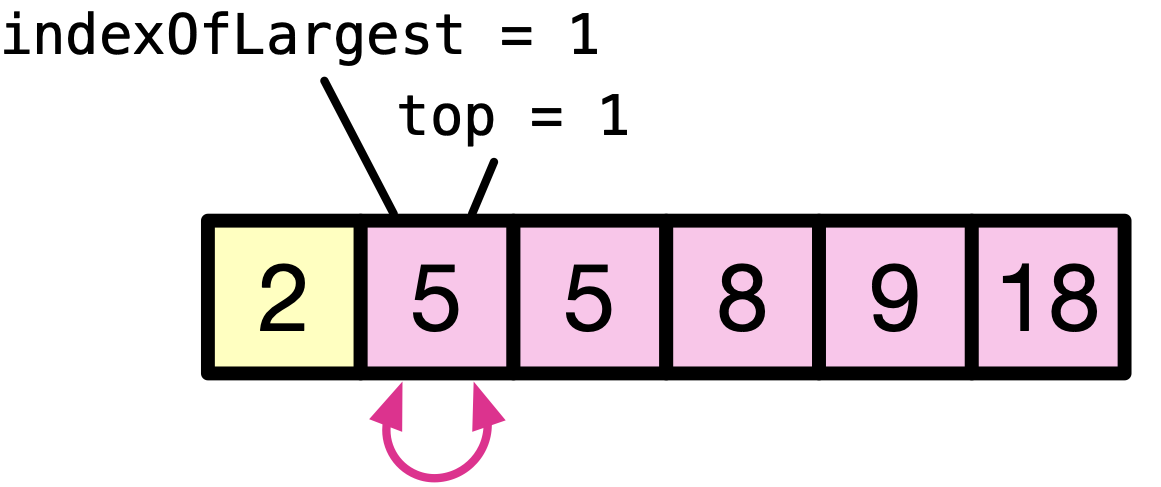
Given the following example array named int A[] = {9, 5, 18, 8, 5, 2};

selection-sort-example

Selection sort works as follows:

  1. Find the maximum element from the unsorted part of the array, which is initially the entire array. Then swap it with the last element.

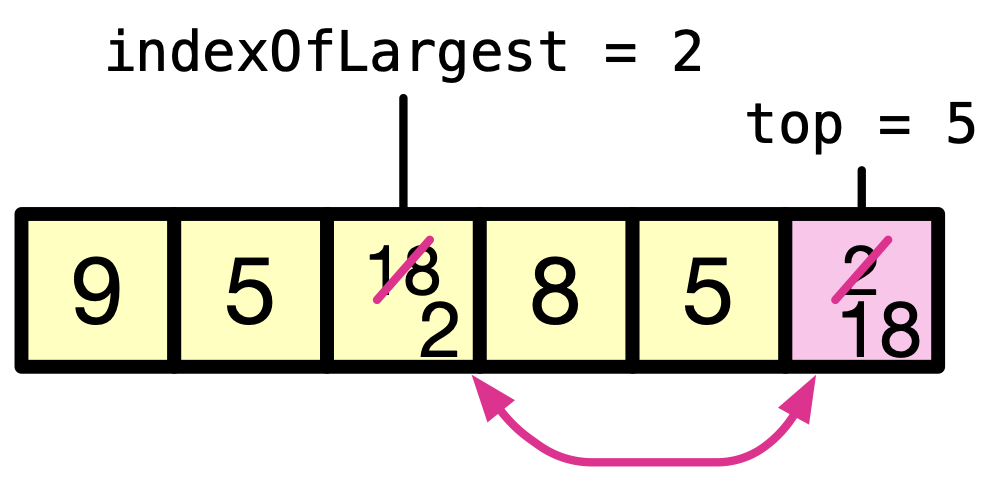
    selection-sort-first-iteration

    After the first iteration, the last element of the array — as a sub-array — is sorted, and is holding the maximum element of the array.

  2. Find the maximum element from the unsorted part of the array, which is the remaining of the array excluding the last element. Then swap it with the last element of the unsorted array. top is holding the index of the last element of the unsorted array.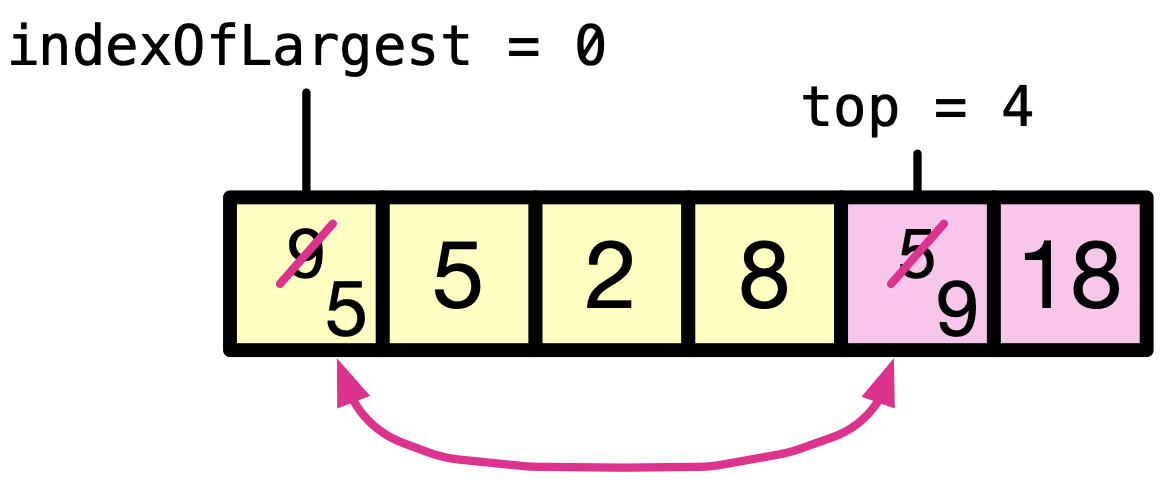

    selection-sort-second-iteration

    After the second iteration, the last two elements of the array — as a sub-array — are sorted, holding the maximum two elements of the array.

  3. If the largest element is also the last element in the unsorted sub-array, we swap the element with itself. After that, the last three elements of the array — as a sub-array — are sorted, holding the maximum three elements of the array.

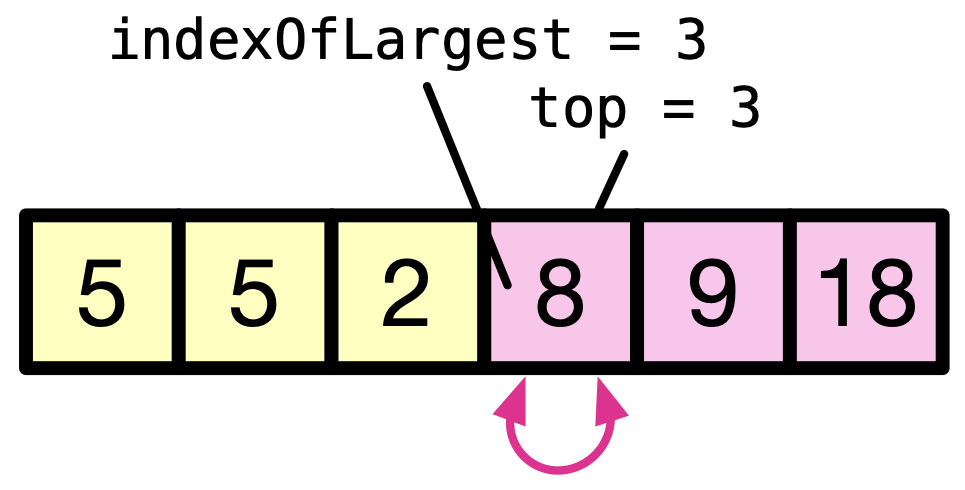
    selection-sort-third-iteration

The process repeats till the entire array gets sorted.

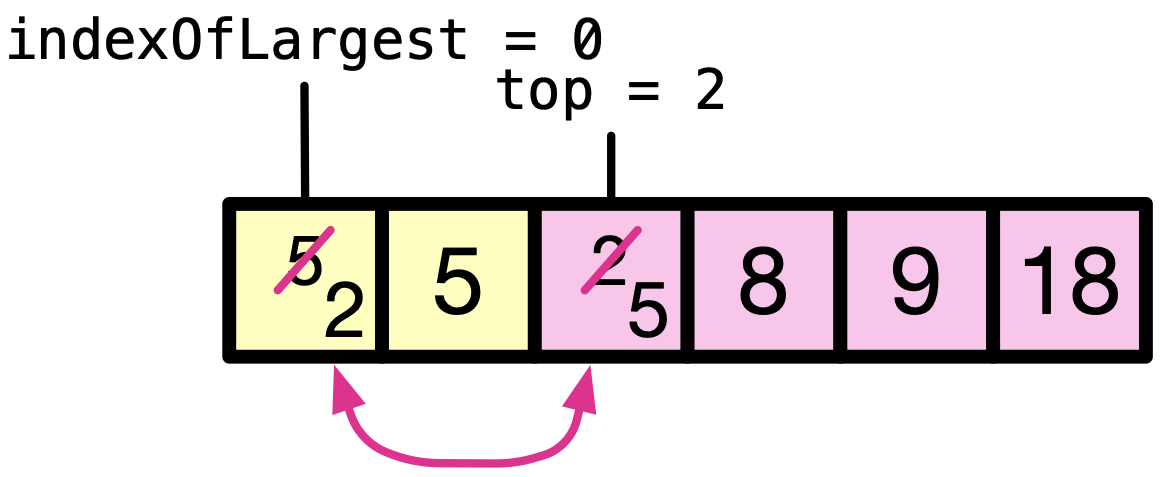
selection-sort-forth-iteration
selection-sort-fifth-iteration

14.2.2. Pseudocode#

We write pseudocode for selection sort as follows:

  1. Set top to n - 1, where n is the length of the array.

  2. Iterate elements from index 0 to top to find the largest element and place its index in indexOfLargest

  3. Swap element at index top with element at index indexOfLargest. This places the largest element at the end of the unsorted sub-array.

  4. Decrement top by 1.

  5. Repeat steps 2 to 4 till top is 0.

14.2.3. Implementation#

We implement selection sort as follows. In lines \(8\) to \(12\), we implement the swap function that swaps two int values. We implemented the swap function before in Section 6.3. Download selection-sort.c if you want to play with the code.

Code 


#include <stdio.h>
void printArray(int list[], int listLength) {
  for (int i = 0; i < listLength; i++) {
    printf("%d ", list[i]);
  }
  printf("\n");
}


void swap(int *x, int *y) {
  int temp = *x;
  *x = *y;
  *y = temp;
}


void selectionSort(int list[], int n) {
  for (int top = n - 1; top > 0; top--) {
    // find largest from 0 to top
    int indexOfLargest = 0;
    for (int i = 1; i <= top; i++) {
      if (list[i] > list[indexOfLargest]) {
        indexOfLargest = i;
      }
    }
    // put largest at top
    swap(&list[indexOfLargest], &list[top]);
    printf("After iteration %d: ", n - top);
    printArray(list, 6);
  }
}


int main(void) {
  int list[] = {9, 5, 18, 8, 5, 2};
  selectionSort(list, 6);
  printArray(list, 6);
}

Quiz

0 Questions

X