Exercises
9.4. Exercises#
Many of these exercises are taken from past exams of APS105 Computer Fundamentals courses at University of Toronto. The solutions are provided in the answer boxes.
Headings in this page classify the exercises into different categories: [Easy], [Intermediate], and [Challenging]. I suggest you start by easy exercises and work your way up to the challenging ones.
Question 10 in Winter 2017 Final Exam [Intermediate]
You are to write a function that sets a rectangular portion of a 2-dimensional array to a specific value. The function takes the following as input parameters: an integer 1000 \(\times\) 1000 2-dimensional array called A, four integer parameters named rowStart, rowEnd, colStart, and colEnd and an integer parameter value.
The purpose of the function is to set the value of the array elements in A beginning with A[rowStart][colStart] and ending with A[rowEnd][colEnd] to be the value value. The
picture below illustrates that the shaded portion of the array should have its elements changed to value, for the specific example given:
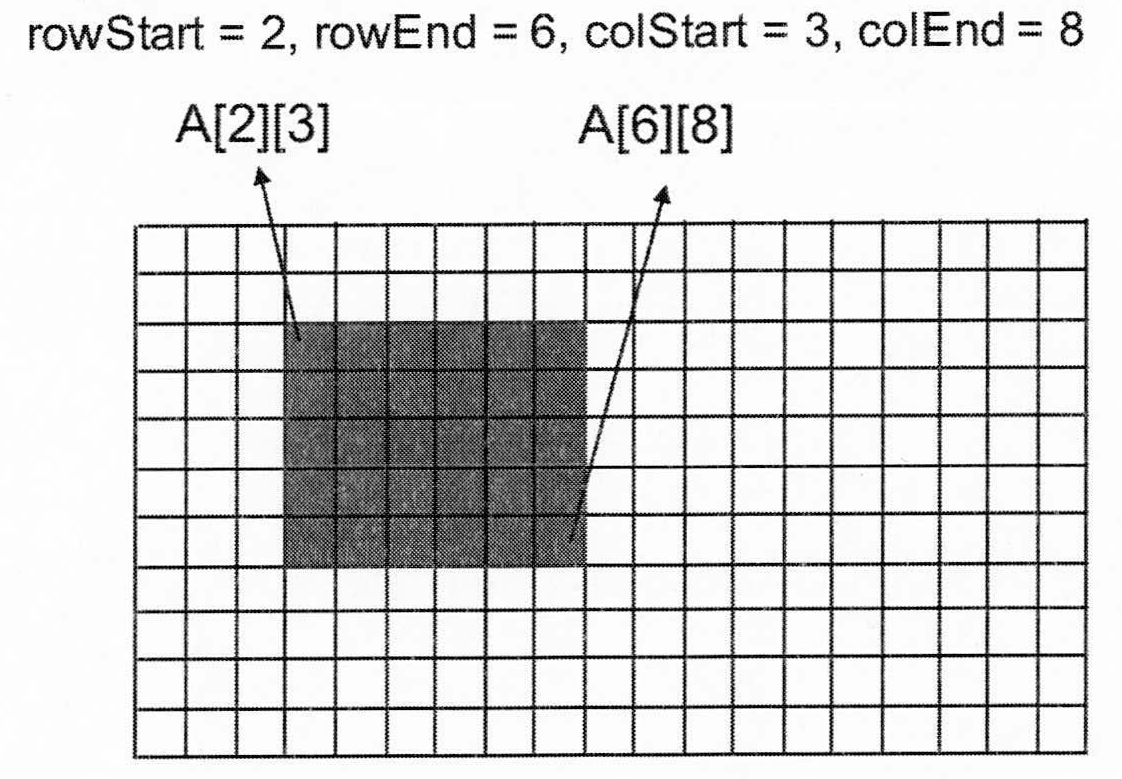
However, this function is to he used by students in a first year C programming course, and those students are well-known for writing code that has errors. For example, they often attempt to access elements of an array outside of its defined bounds, among other problems. Therefore, your function should check that the inputs to the function are correct before performing the above operation. You must determine, through the reading of this question, what would make the inputs rowStart, rowEnd, colStart, colEnd and value correct. (You can assume that the array A is passed in correctly.)
The function should return a boolean result that is set to true if the inputs are valid, and false if they are not. In the case that the inputs are not valid, the setting of the values of the array should not be attempted.
IMPORTANT: Your solution, in addition to the code for the function described above, should also show how you would call this function from the main function, and make use of its return value. That is, you should show the call to the function (with appropriately declared variables, and gathering input from the user for rowStart, rowEnd, colStart, colEnd and value) and make appropriate use of the returned boolean value.
Answer
#include <stdbool.h>
#include <stdio.h>
bool checkBound(int start, int end) {
// not every check here is strictly necessary
if (start > end) return false;
if (start < 0 || start > 999) return false;
if (end < 0 || end > 999) return false;
return true;
}
bool initSectionInArray(int A[1000][1000], int rowStart, int rowEnd,
int colStart, int colEnd, int value) {
if (!checkBound(rowStart, rowEnd)) return false;
if (!checkBound(colStart, colEnd)) return false;
for (int i = rowStart; i <= rowEnd; i++)
for (int j = colStart; j <= colEnd; j++) A[i][j] = value;
return true;
}
int main(void) {
int x1, x2, y1, y2, v, a[1000][1000];
printf("Enter x1, x2, y1, y2, v\n");
scanf("%d%d%d%d%d", &x1, &x2, &y1, &y2, &v);
if (initSectionInArray(a, x1, x2, y1, y2, v))
printf("Success!\n");
else {
printf("Failure - something wrong with input indices\n");
return (1);
}
return 0;
}
Question 9 in Winter 2022 Final Exam [Intermediate]
Write a C function called borderSum that adds all the border elements of the top-left 2D \(n \times n\) square matrix inside a 2D square array. For example, for the array below, if n is 3, we should add {1, 2, 3, 7, 11, 10, 9, 5} and return 48. If n is 0, the function should return 0. If n is 1, the function should return the top-left element, which is 1 for the array below.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
The header of the borderSum function is provided below, where 26 is the number of rows and columns in the 2D array mat, and n is the size of the square matrix to which we need to get the sum of its border. You can safely assume n \(\leq\) 26.
int borderSum(int mat[][26], int n){
Answer
Solution 1.
int borderSumAlt(int mat[][26], int n) {
int sum = 0;
if (n == 0)
return 0;
else if (n == 1)
return mat[0][0];
else {
for (int i = 0; i < n; i++)
sum += mat[i][0] + mat[0][i] + mat[n - 1][i] + mat[i][n - 1];
}
return sum - mat[0][0] - mat[n - 1][n - 1] - mat[0][n - 1] - mat[n - 1][0];
}
Solution 2.
int borderSum(int mat[][26], int n) {
int sum = 0, row, col;
if (n == 0) {
return 0;
} else if (n == 1) {
sum = mat[0][0];
} else if (n == 2) { //unnecessary else-if, but fine if it is there
sum = mat[0][0] + mat[0][1] + mat[1][0] + mat[1][1];
} else {
for (col = 0; col < n; col++) {
sum += mat[0][col] + mat[n - 1][col];
}
for (row = 1; row < n - 1; row++) {
sum += mat[row][0] + mat[row][n - 1];
}
}
return sum;
}
Question 4 in Winter 2020 Final Exam [Intermediate]
For artificial intelligence (AI) that uses recently developed “neural network” techniques, layers of “neurons” pass their values, weighted by multipliers, into the next layers. Finding those weights is, of course, the more difficult and computationally intensive part, but once you have them, the use is relatively simple array multiplication.
Here we will work with two layers to do the last stages and to compute values for the output. For example, the output could be the likelihood that the inputs are from the picture of one of four animals: dog, cat, pig, beaver. This net will “recognize” which of these it is by choosing the output of highest value. Here is a diagram that represents what we are doing:
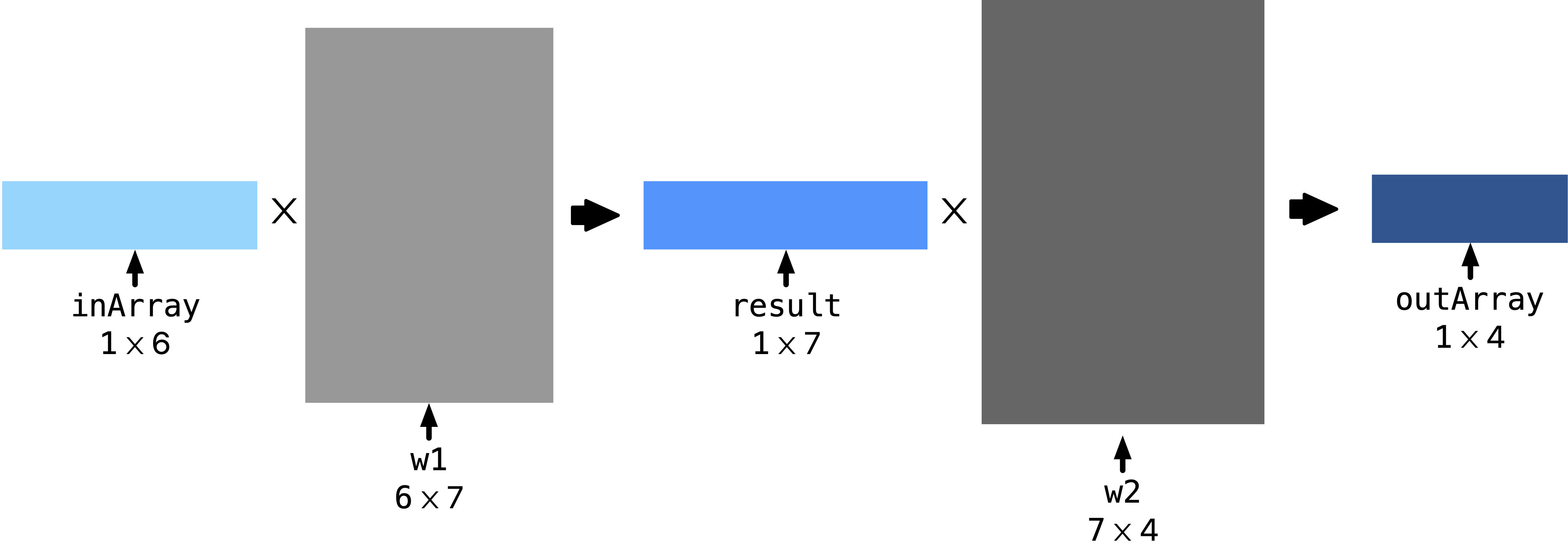
You will generate the function to perform the operation shown starting with the code below that includes the w1 and w2 weight arrays and that takes an input array. The input is one-dimensional, size 6. w1 and w2 are two-dimensional: w1 is \(6\) by \(7\). w2 is \(7\) by \(4\). The output is
one-dimensional and of size \(4\).
Note: To multiply a N\(\times\)1 array A, by an M\(\times\)N array B, to get an M\(\times\)1 array C:
C[0] = A[0] * B[0,0] + A[1] * B[0,1] + A[2] * B[0,2] + ... + A[N-1] * B[0,N-1] C[1] = A[0] * B[1,0] + A[1] * B[1,1] + A[2] * B[1,2] + ... + A[N-1] * B[1,N-1] ... C[M-1] = A[0] * B[M-1, 0] + A[1] * B[M-1, 1] + A[2] * B[M-1, 2]+ ... + A[N-1] * B[M-1, N-1]
Here is the function to finish:
#include <stdio.h>
// this function uses a one-dimensional input array of size 6, and
// puts values into the one-dimensional output array of size 4
void performAI(double *inArray, double *outArray) {
// these are the weighting arrays as in the diagram
double w1[6][7] = {{0.795279571, 0.565454091, 0.569392801, 0.649519912,
0.311228459, 0.869033219, 0.963890145},
{0.261182548, 0.967901447, 0.015463096, 0.101966965,
0.454071297, 0.396147575, 0.853833996},
{0.976180547, 0.762522649, 0.223067359, 0.120228416,
0.710471648, 0.220771538, 0.052876278},
{0.173285965, 0.795507616, 0.258332188, 0.813302777,
0.528470338, 0.885245811, 0.190564347},
{0.14018923, 0.324797853, 0.012649753, 0.928397252,
0.048519668, 0.321836138, 0.360198988},
{0.063248883, 0.72395506, 0.606492812, 0.435057638,
0.462896967, 0.12061378, 0.28806367}};
double w2[7][4] = {{0.036340161, 0.702081192, 0.406643568, 0.383400727},
{0.786459022, 0.627286192, 0.190417846, 0.259622675},
{0.996272492, 0.115783107, 0.922042574, 0.805576672},
{0.254649714, 0.818737484, 0.23760355, 0.884876231},
{0.587934606, 0.566762923, 0.254228386, 0.735145224},
{0.709219708, 0.815306359, 0.395073347, 0.191438772},
{0.743663242, 0.969784133, 0.055612809, 0.992284824}};
// TODO: your code here
};
Here is an example use of the function.
double inData[] = {10, 11, 14, 51, 22, 24};
double outData[4];
performAI(inData, outData);
Answer
void performAI(double *inArray, double *outArray) {
// these are the weighting arrays as in the diagram
double w1[6][7] = {{0.795279571, 0.565454091, 0.569392801, 0.649519912,
0.311228459, 0.869033219, 0.963890145},
{0.261182548, 0.967901447, 0.015463096, 0.101966965,
0.454071297, 0.396147575, 0.853833996},
{0.976180547, 0.762522649, 0.223067359, 0.120228416,
0.710471648, 0.220771538, 0.052876278},
{0.173285965, 0.795507616, 0.258332188, 0.813302777,
0.528470338, 0.885245811, 0.190564347},
{0.14018923, 0.324797853, 0.012649753, 0.928397252,
0.048519668, 0.321836138, 0.360198988},
{0.063248883, 0.72395506, 0.606492812, 0.435057638,
0.462896967, 0.12061378, 0.28806367}};
double w2[7][4] = {{0.036340161, 0.702081192, 0.406643568, 0.383400727},
{0.786459022, 0.627286192, 0.190417846, 0.259622675},
{0.996272492, 0.115783107, 0.922042574, 0.805576672},
{0.254649714, 0.818737484, 0.23760355, 0.884876231},
{0.587934606, 0.566762923, 0.254228386, 0.735145224},
{0.709219708, 0.815306359, 0.395073347, 0.191438772},
{0.743663242, 0.969784133, 0.055612809, 0.992284824}};
double midarray[7];
int i, j;
for (i = 0; i < 7; i++) {
midarray[i] = 0.0;
for (j = 0; j < 6; j++) {
midarray[i] += inArray[j] * w1[j][i];
}
}
for (i = 0; i < 4; i++) {
outArray[i] = 0.0;
for (j = 0; j < 7; j++) {
outArray[i] += midarray[j] * w2[j][i];
}
}
}
Question 11 in Fall 2015 Final Exam [Challenging]
Pictures that come from a smartphone camera can be represented as a two-dimensional array of numbers, where each number corresponds to the colour of each pixel in the picture. These cameras suffer from various effects that cause errors in the colour they measure (this variation is often called ‘noise’) which makes the picture have poor quality. One way to reduce that noise is to average each pixel with the eight pixels that surround it.
In this question, you will write a C-language function that takes in such an image as an array, A, of 100 by 100 of double-type numbers. It computes the ‘averaged’ array, B, which is a slightly smaller 98 by 98 array in which each element is the computed average of 9 pixels in the input array.
The figure below illustrates the computation for a smaller example version of A (a 6 \(\times\) 6 array) that would produce a 4 \(\times\) 4 array B. (The reason that B is smaller than A by 2 is that, at the edges of A, there are not enough “surrounding” pixels to produce a full result for B).
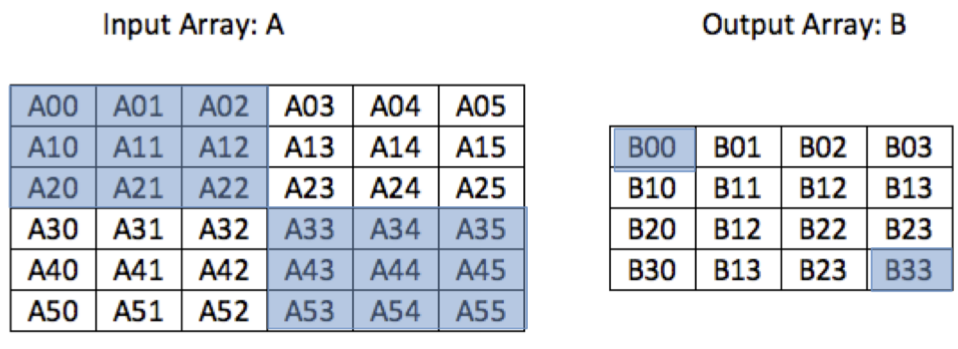
The computation can also be described by these examples: the element B00 of the output array B is computed as the arithmetic average of the 9 elements of A that are shaded in the upper left corner of array A in the above figure. That is, B00 is the average the nine elements surrounding and including element A11 (i.e. A00, A01, A02, A10, A11, A12, A20, A21, A22). Similarly, B01
is the average of the 9 elements surrounding and including A12. B02 is the average of the 9 surrounding/including to A13. B10 is the average of the 9 surrounding/including A21. As a final example, B33 is the average of the 9 surrounding/including A44, the set of which is illustrated as the shaded section of the lower right hand set of values in the array A above.
You are to write a C function with a prototype as follows:
void averageImage(double A[100][100], double B[98][98]);
Where A is the input array, and B is the array that the function computes. A specific requirement is that you must use one or more loops to compute the average of the 9 elements of A. That is, you must not explicitly write out the sum of nine separate elements of A to compute each element of B.
Answer
void averageImage(double A[100][100], double B[98][98]) {
double sum;
for (int i = 0; i < 98; i++) {
for (int j = 0; j < 98; j++) {
sum = 0.0;
for (int k = 0; k < 3; k++) {
for (int m = 0; m < 3; m++) sum = sum + A[i + k][j + m];
}
B[i][j] = sum / 9.0;
}
}
}
Question 15 in Fall 2014 Final Exam [Challenging]
Consider the C program given, in part, below. It declares an integer array of dimensions SIZE \(\times\) SIZE, where SIZE is a defined constant as shown. The first part of the main program calls the fillArray function which sets each element of the array to the value \(0\), \(1\), or \(2\). The program then asks the user to provide a value, \(n\), which must be an odd integer. (You can assume that the user does enter an odd number, and that n >= 1 and n <= SIZE.) The goal of the program is to find all patterns of crosses of size n in the array of all 1 or 2. For example, in the array shown below the code, there is a cross of size n = 3 of 1 centered at indices row = 2, column = 4, a cross of size n = 3 of 2 centered at indices row = 5, column = 8, and another one centered at indices row = 6, column = 2.
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
#define SIZE 10
int main(void) {
int array[SIZE][SIZE];
int n;
fillArray(array);
printf("Enter Cross Size to search (must be odd): ");
scanf("%d", &n);
// Your main program code would go here
return 0;
}
Example array:

The output of program is as follows, if the array above was the input, and n = 3:
Found Cross of Size 3 of 1 at (2,4) Found Cross of Size 3 of 2 at (5,8) Found Cross of Size 3 of 2 at (6,2)
Your answer should consist of the code that goes inside the main program above, and additional functions. Your answer must make use of at least one function. You do not need to rewrite the C code provided to you in the space below.
Answer
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
#define SIZE 10
int main(void) {
int array[SIZE][SIZE];
int n;
fillArray(array);
printf("Enter Cross Size to search (must be odd): ");
scanf("%d", &n);
for (int row = 0; row < SIZE; row++)
for (int col = 0; col < SIZE; col++) {
if (findCross(array, n, 1, row, col))
printf("Found Cross of Size %d of %d at (%d,%d)\n", n, 1, row, col);
if (findCross(array, n, 2, row, col))
printf("Found Cross of Size %d of %d at (%d,%d)\n", n, 2, row, col);
}
return 0;
}
bool findCross(int array[SIZE][SIZE], int n, int searchNum, int row, int col) {
/* look across one column */
bool found = true;
int start, end;
start = row - n / 2;
end = row + n / 2;
// first check if size precludes the result
if (start >= 0 && end < SIZE) {
// now look and see if the right number in a row
for (int k = start; k <= end && found; k++)
if (array[k][col] != searchNum) found = false;
} else
found = false;
// look across row
start = col - n / 2;
end = col + n / 2;
// first check if size precludes the result
if (start >= 0 && end < SIZE) {
// now look and see if the right number in a column
for (int k = start; k <= end && found; k++)
if (array[row][k] != searchNum) found = false;
} else
found = false;
return found;
}
