Binary representation in memory
Contents
1.2. Binary representation in memory#
The memory stores data and program instructions in binary format, i.e. 0s and 1s. How does this look like? Let’s take a closer look at what the memory has.
Binary is a base-2 number system. It allows two states (0 and 1) to represent a digit. This is different from the decimal/base-10 number system that allows ten states (0 – 9) for each digit. The smallest unit of binary number is a bit. A bit can be a 0 or a 1.
Let’s start representing decimal numbers using bits. It is intuitive to represent a decimal 0 with a binary 0 and a decimal 1 with a binary 1.
How about other decimals? In the decimal number system, after 9 comes 10. This adds 1 to the ten’s digit, and the one’s digit is reset to 0. Similarly, we can add 1 to the next significant digit and set the lowest significant digit to 0. For example, we can represent a decimal 2 with a binary 10. Higher significant numbers are towards the left, just like in decimal number system. Let’s name this higher significant bit “two’s bit”, and the lowest significant digit “one’s bit”.
Representing a decimal 3 requires adding 1 to the ones significant bit. This gives us 11. The following table summaries the binary representation of decimal numbers from 0 to 3.
Decimal |
Binary |
|---|---|
0 |
00 |
1 |
01 |
2 |
10 |
3 |
11 |
For numbers greater than 3, again we need a 1 in another higher significant digit to the left – four’s bit. The remaining bits to the right (two’s and one’s digits) are set to 0. This gives us 100, which is the binary representation of decimal 4. The same logic follows for more numbers. The following table shows the binary representation of decimal numbers from 0 to 7.
Decimal |
Binary |
|---|---|
0 |
000 |
1 |
001 |
2 |
010 |
3 |
011 |
4 |
100 |
5 |
101 |
6 |
110 |
7 |
111 |
1.2.1. How to know the decimal number from a binary number?#
To convert a binary number to a decimal number, we need to know the value of each bit. In the previous section, we discussed the logic behind representing decimal numbers in binary. We can use the same logic to convert a binary number to a decimal number.
In decimal numbers, we have the one’s digit, ten’s digit, hundred’s digit and so on. The value of each digit is the power of \(10\). One’s digit is \(10^0\), ten’s digit is \(10^1\), hundred’s digit is \(10^2\) and so on. Similarly, in binary numbers, we have the one’s bit, two’s bit, four’s bit and so on. The value of each bit is the power of \(2\). The value of the one’s bit is \(2^0\), the value of the two’s bit is \(2^1\), the value of the four’s bit is \(2^2\) and so on.
To be able to get the decimal equivalent of a binary representation, we need to multiply each bit with its value. For example, the binary number 101 is equivalent to \(1 \times 2^0 + 0 \times 2^1 + 1 \times 2^2 = 5\). Another example is shown in the following figure.
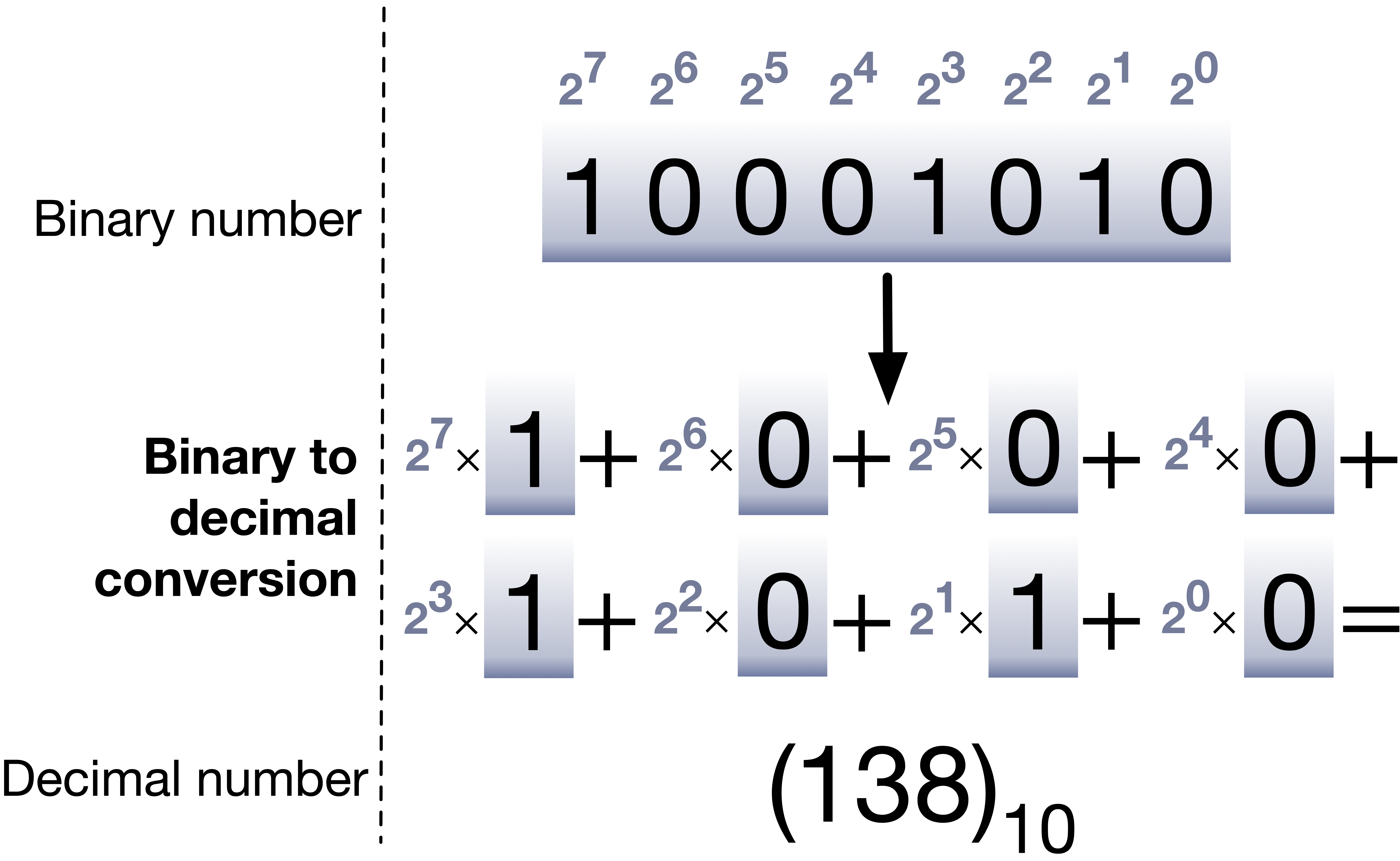
Fig. 1.2 Binary to decimal conversion example#
1.2.2. How to know the binary representation of a decimal number?#
While we discussed earlier the logic of developing the binary representation from decimal numbers, we need to find a way to convert individual decimals to their binary representation.
The main idea is the following: In the binary to decimal conversion, we had to multiply each bit with its value. To reverse this, in the decimal to binary conversion, we need to divide the decimal number by two repeatedly to know the value we need to put in each bit.
The method. For example, we have 138 to convert to binary. We divide 138 by 2 and get a quotient of 69 and a remainder of 0. We continue dividing the quotient by 2, and keep track of remainders. This stops when the quotient reaches 0. The last remainder is the highest significant bit, and the first is the lowest significant bit. The following figure shows the steps of the conversion through an example.
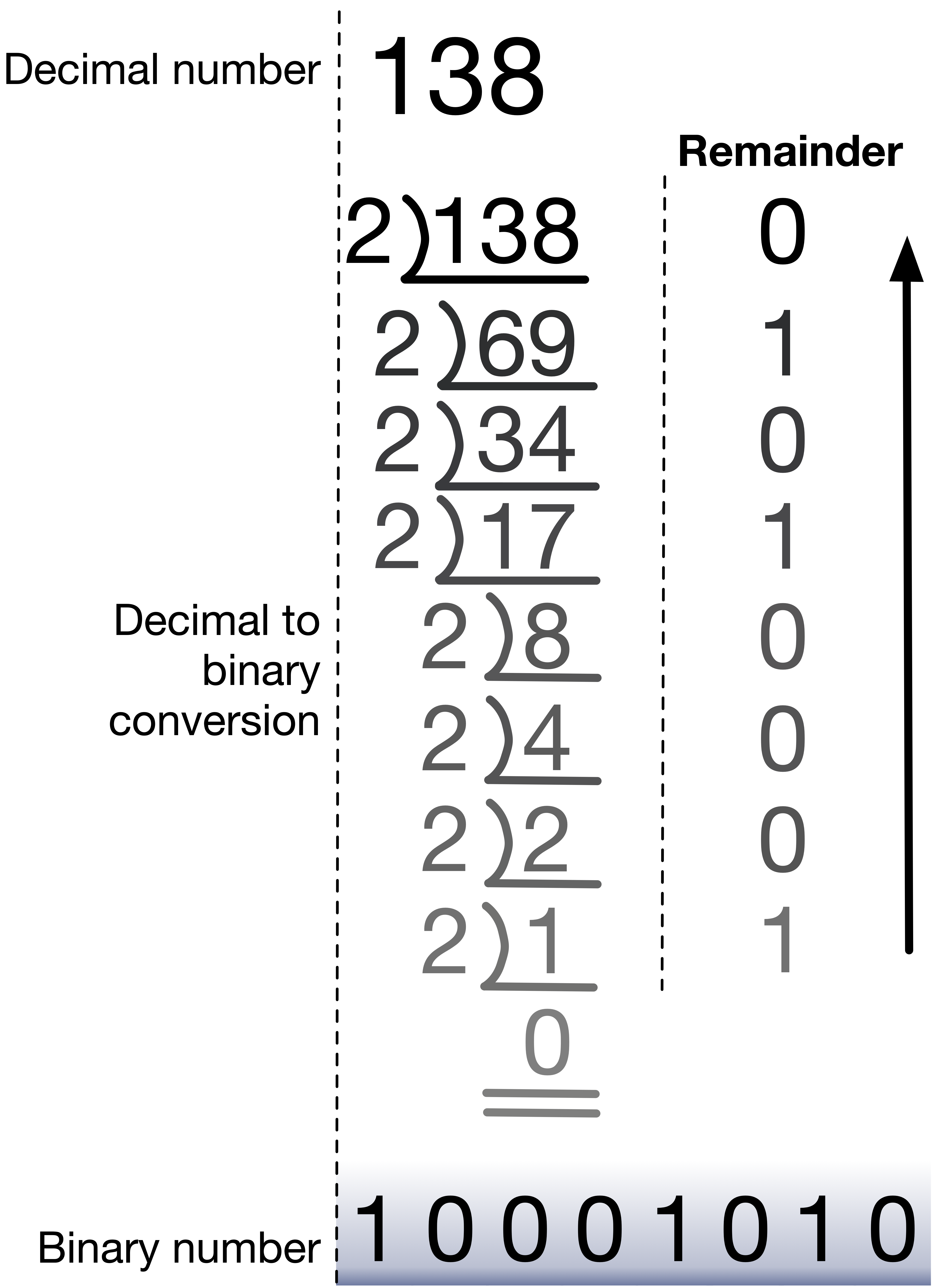
Fig. 1.3 Decimal to binary conversion example#
1.2.3. How many bits do we need to represent \(x\) numbers?#
So far we used
1- One bit to represent 2 numbers (0 and 1).
2- Two bits (two’s and one’s bits) to represent 4 numbers (0 to 3).
3- Three bits (four’s, two’s and one’s bits) to represent 8 numbers (0 to 7).
We can see a pattern here. We need \(n\) bits to represent \(2^n\) numbers. A byte is a group of 8 bits. Hence, a byte can store \(2^8 = 256\) different numbers.
To represent \(x\) numbers, we need \(\log_2(x)\) bits. For example, to represent 256 numbers, we need 8 bits. To represent 512 numbers, we need 9 bits. To represent 1024 numbers, we need 10 bits.
Note
A byte is a group of 8 bits. A kilobyte (KB) is 1024 bytes. A megabyte (MB) is 1024 kilobytes. A gigabyte (GB) is 1024 megabytes. A terabyte (TB) is 1024 gigabytes.
1.2.4. How is the 0s and 1s of data memory organized?#
The memory is organized in cells. Each cell stores a byte. Each cell has an address. This makes the memory byte-addressable. This means at each address only one byte is stored.
Since the computer only understands 0s and 1s, we will use binary format to refer to the addresses. For example, the address 0000 refers to the first cell in the memory. The address 0001 refers to the second cell in the memory. The address 0010 refers to the third cell in the memory.
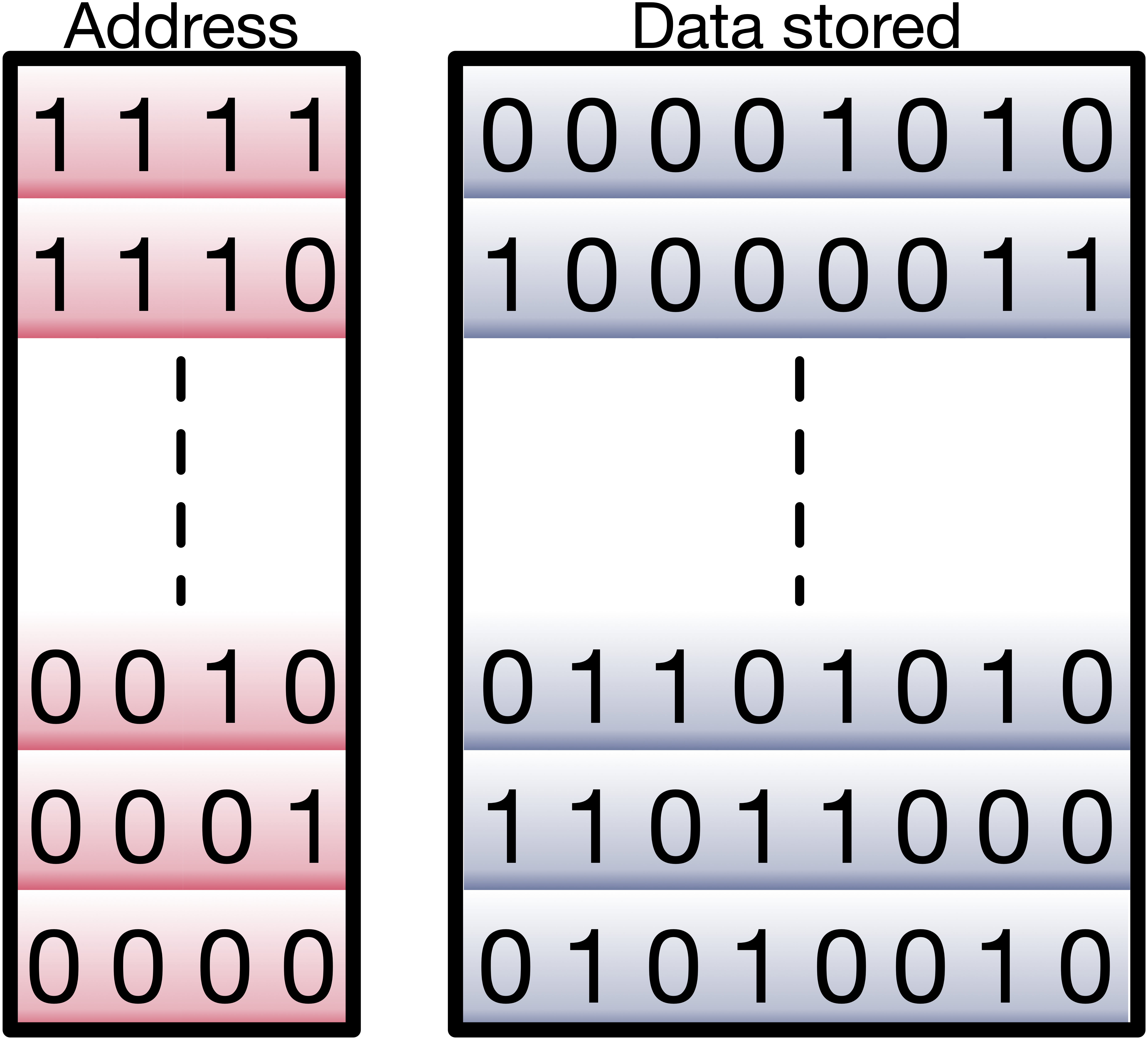
Fig. 1.4 The byte addressable memory#
How many bytes can be stored in the memory, if we use 32 bits to represent the address? We can use the formula \(2^n\) to calculate this. Since we have 32 bits, we can represent \(2^{32}\) numbers. This means we can store \(2^{32}\) bytes in the memory.
How much is \(2^{32}\) bytes? Let’s breakup \(2^{32}\) into \(2^2 \times 2^{10} \times 2^{10} \times 2^{10}\). As we said before, \(2^{10}\) is 1024 bytes, which is a kilobyte. So \(2^{10} \times 2^{10}\) makes 1024 \(\times\) kilobyte = megabyte. And \(2^{10} \times 2^{10} \times 2^{10}\) makes 1024 \(\times\) megabyte = gigabyte. So \(2^{32}\) bytes is 4 gigabytes. That’s not too much.
Modern computers use 64-bits to represent their addresses. How many bytes can a 64-bit address represent? \(2^{64}\) bytes is 16 exabytes. That’s a lot of memory!
Now, that we know how is the data represented inside the main memory and how is each byte addressed, let’s see the cycle of developing a program in C.
Quiz
0 Questions
