Math library
Contents
2.4. Math library#
In the previous section, we study simple arithmetic operations. Operations in real life will be more complicated, such as finding the logarithm of a number. In this section, we will learn about a math library that provides us access to complicated operations, such as \(\log\), \(\tan\), \(\sin\), \(\cos\) and many more.
2.4.1. Complicated math operations#
For example, we want to get the hypotenuse of a right-angled triangle with sides \(a\) and \(b\). The hypotenuse is the longest side of the right-angled triangle. The hypotenuse is given by the formula: \(c = \sqrt{a^2 + b^2}\). Since, a square root is a complicated operation, we use the math library to get the square root of a number.
We use sqrt function to get the square root of a number. A function has inputs and outputs. sqrt has input or receives a double and has output or returns the square root of the input in double type, as shown in the following figure. We can also say double sqrt(double x) to represent the input as double (between brackets), and output as double, written before sqrt.
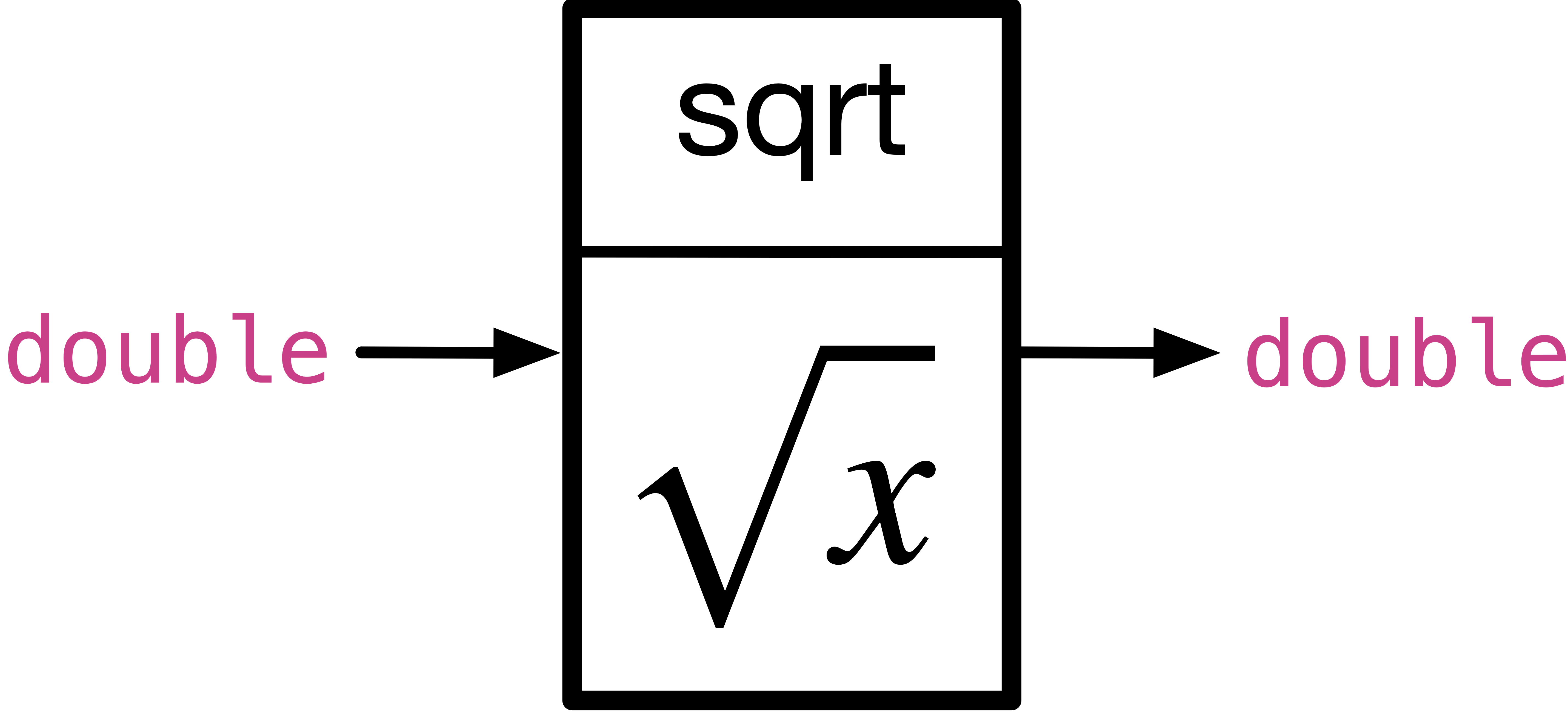
Fig. 2.2 sqrt function in math library with prototype double sqrt(double x)#
Line 1 includes the math library, without which we can not use math library functions. Line 11 in the following code uses sqrt function to get the square root of \(a^2 + b^2\). Download hypotenuse.c to get the following code.
Code
#include <math.h> #include <stdio.h>
int main(void) { double a = 0, b = 0, c = 0; printf("Enter the length of the first side: "); scanf("%lf", &a); printf("Enter the length of the second side: "); scanf("%lf", &b);
c = sqrt(a * a + b * b); printf("The length of the hypotenuse is %.2lf\n", c); return 0; }
Want fewer lines? You can also write the above code in fewer lines as shown below.
Code
1#include <math.h>
2#include <stdio.h>
3
4int main(void) {
5 double a = 0, b = 0, c = 0;
6 printf("Enter the lengths of the sides: ");
7 scanf("%lf %lf", &a, &b);
8
9 c = sqrt(a * a + b * b);
10 printf("The length of the hypotenuse is %.2lf\n", c);
11 return 0;
12}
Output
Enter the lengths of the sides: 2.5 4.1 The length of the hypotenuse is 4.80
Line 7 shows us how can scanf allow entry of more than one variable at a time. This is given that the inputs are separated using a space, return or tab. For example, 2.5 ad 4.1 were separated using a space. The space, return or tab are called delimiters when they specify boundaries between separate values.
2.4.2. You can still use integer values#
You can use sqrt in the following use cases:
It can accept an
inttoo. In line 4 in the following code, implicit type conversion fromint2todouble2.0will occur. The output will beSquare root of 2 is 1.41.Code
#include <math.h> #include <stdio.h> int main(void){ printf("Square root of 2 is %.2lf\n", sqrt(2)); return 0; } The output can be stored in an
inttoo. In line 4 in the following example, the value returned fromsqrt(3.0)– 1.73205… – will be truncated and stored invalas1.Code
#include <math.h> #include <stdio.h> int main(void){ int val = sqrt(3.0); return 0; }
2.4.3. Other math library functions#
Some of the relevant math library functions are listed below.
Mathematical notation |
Function Prototype |
What does it do? |
Example |
|---|---|---|---|
\(\sqrt{x}\) |
|
returns the square root of |
|
\(x^y\) |
|
returns |
|
\(e^x\) |
|
returns |
|
\(\log_{10}x\)1 |
|
returns the logarithm to the base 10 of |
|
\(\ln(x)\) |
|
returns the natural logarithm of |
|
\(\mid x \mid\) |
|
returns the absolute value of |
|
\(\sin(x)\) |
|
returns the sine of |
|
\(\cos(x)\) |
|
returns the cosine of |
|
\(\tan(x)\) |
|
returns the tangent of |
|
\(\sin^{-1}(x)\) or \(\arcsin(x)\) |
|
returns the arc sine of |
|
\(\cos^{-1}(x)\) or \(\arccos(x)\) |
|
returns the arc cosine of |
|
\(\tan^{-1}(x)\) or \(\arctan(x)\) |
|
returns the arc tangent of |
|
\(\max(x)\) |
|
returns the maximum of |
|
\(\min(x)\) |
|
returns the minimum of |
|
\(\lfloor x \rfloor\) |
|
returns the greatest integer that is less than or equal to |
|
\(\lceil x \rceil\) |
|
returns the smallest integer that is greater than or equal to |
|
\(x \mod y\) |
|
returns the remainder4 of |
|
\(\lfloor x \rceil\) |
|
returns the nearest integer to x, i.e., rounds |
|
2.4.4. Example use cases for math library functions#
Exercise 1
Write a program that takes in from a user a floating point number and rounds it to the nearest 10th, i.e., first decimal place.
Step 1: Toy example. To understand the problem, we need to start by thinking of a toy example. For example, \(2.18\) rounded to the first decimal place is \(2.2\).
Step 2: Think of a solution. However, rint function only rounds to the nearest integer, not to the nearest decimal places. So, we need to think of a solution that will round to the nearest decimal places.
Step 3: Decompose solution into steps. The trick is to get the decimal place into the integer part. For example, we can move the first decimal to the integer part from \(2.18\) to \(21.8\). Now, we can use rint to round to the nearest integer, which makes \(22.0\). Moving the decimal back gets us \(2.2\), which is what we want.
Step 4 (optional, but very helpful): Draw your solution.
Fig. 2.3 Trials into developing a solution for rounding to the nearest 10th.#
Step 5: Make sure your steps works on other toy examples. For example, try testing your code with a negative number or a umber where the first decimal place is above \(5\). Try whatever you think might break your code. E.g. \(-1.87 \times 10 = -18.7\), rint(-18.7) returns -19.0, then finally \(-19.0 / 10 = -1.9\), which is what we want.
Step 6: Write the code.
Download nearest10.c to get the following code.
Code
#include <math.h> #include <stdio.h>
int main(void) { double n = 0; printf("Enter the number you want to round to the nearest 10th: "); scanf("%lf", &n);
n = rint(n * 10) / 10; printf("The number rounded to the nearest 10th is %.1lf\n", n); return 0; }
Exercise 2
Canada does not have pennies. The lowest value coin is a nickel, which is worth 5 cents. Write a program that takes in from a user a floating point number price and rounds it to the nearest nickel.
Step 1: Toy example. \(2.94\) when rounded to the nearest nickle is \(2.95\). \(2.92\) when rounded to the nearest nickle is \(2.90\). \(1.98\) is \(2.00\). \(7.83\) is \(7.85\).
Step 2: Think of a solution. We can use a similar trick as in Exercise 1. However, if we do the same as in Exercise 1, we will round to the nearest dime, which is 10 cents. Example, \(2.94 \times 10\) \(\rightarrow\) \(29.4\). 29.4 is the number of 10 cents in \(\$2.95\). rint(29.4) \(\rightarrow\) \(29.0\) \(\rightarrow\) \(29.0 / 10\) \(\rightarrow\) \(2.9\). That is not what we want! We want to \(2.95\).
Step 3: Decompose solution into steps. We need to round to the nearest nickel, which is 5 cents. So, we need to get the number of nickles in \(2.94\), and round that decimal number to the nearest whole nickle. For example, \(2.94 \times 100 / 5\) \(\rightarrow\) \(58.8\). 58.8 is the number of nickles in \(\$2.94\). rint(58.8) returns \(59.0\) nickles, which make \(59.0 \times 5 / 100\) \(\rightarrow\) \(\$2.95\). This is what we want!
Step 4 (optional, but very helpful): Draw your solution.
Fig. 2.4 Trials into developing a solution for rounding to the nearest nickle.#
Step 5: Make sure your steps works on other toy examples. For example, where the nearest nickle changes the entire number as \(1.98\). \(1.98 \times 100 / 5 = 39.6\), rint(39.6) returns 40.0, which makes \(40.0 / 100 \times 5 = 2.0\), which is \(1.98\) rounded to the nearest nickle.
Step 6: Write the code.
Download nearest-nickle.c to get the following code.
Code
#include <math.h> #include <stdio.h>
int main(void) { double price = 0; printf("Enter the amount to round to the nearest nickle: "); scanf("%lf", &price); printf("$%.2lf rounded to the nearest nickle is $%.2lf\n", price, rint(price * 100 / 5) / 100 * 5); return 0; }
Quiz
0 Questions
- 1
To get the \(\log_{n}(x)\), \(\log\) base \(n\) of \(x\), where \(n\) is any number, recall you can always use the following \(\log_{n}(x) = \frac{\log_{10} (x)}{\log_{10} (n)}\). In C,
log10(x)/log10(n)to calculate \(\log_{n}(x)\).- 2
M_Eis a constant defined in math library, denoting the value of constant \(e\). It is approximately equal to 2.718281828…- 3(1,2,3)
M_PIis a constant defined in math library, denoting the value of \(\pi\). It is approximately equal to 3.14159…- 4
How do we get remainders for floating point numbers? For example, \(\frac{5.3}{2.1}\) yields \(2.523...\). To get the remainder of this division, we remove the whole number \(2\) from \(2.523...\), and we are left with \(0.523...\). The remainder would be \(0.523... \times 2.1\). Hence,
fmod(5.3, 2.1)is \(1.1\).
