Binary Search
Contents
15.2. Binary Search#
Searching for an element in a sorted array is quick. Think of having a pile of booklets with names sorted in ascending order. Say you want to find the booklet with the name “Snefru”. You can start at the middle of the pile and check if the name is “Snefru”. If it is, you are done. If it is not, you can check if the name is before or after “Snefru”. If it is before, you can discard the second half of the pile. If it is after, you can discard the first half of the pile. You can repeat this process until you find the booklet with the name “Snefru”.
This method that we just discussed is called binary search. It is called binary search because it searches the list in a binary fashion, checking the middle element of the list and then discarding half of the list based on the result.
Given an array of seven elements named list as shown in the figure below, we want to look for item \(9\).
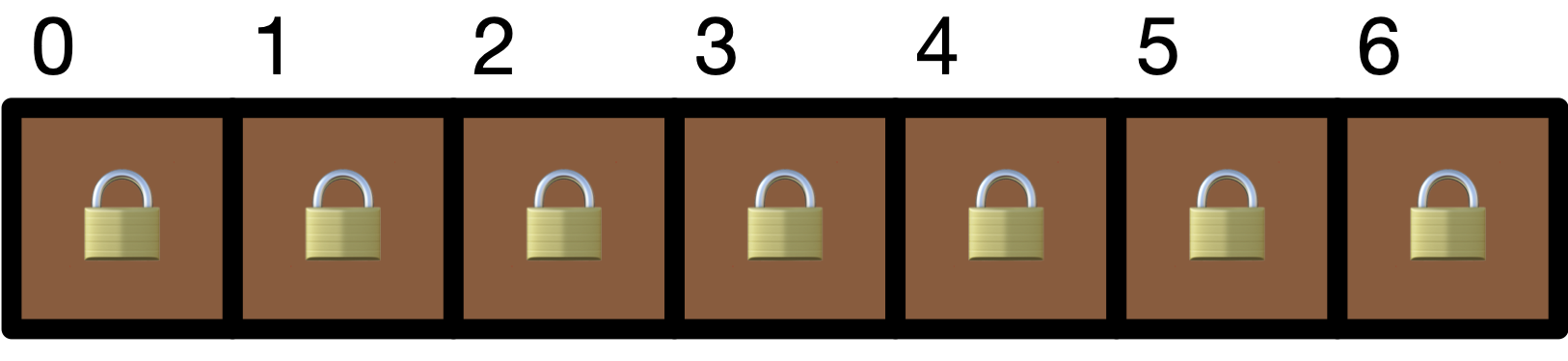
The algorithm for binary search is as follows:
Define the limits of the array using variables
lowandhigh. We can do so by initially settinglow = 0andhigh =length of array- 1. Since we want to look at the middle element, we can hold its index inmiddle = (low + high)/2.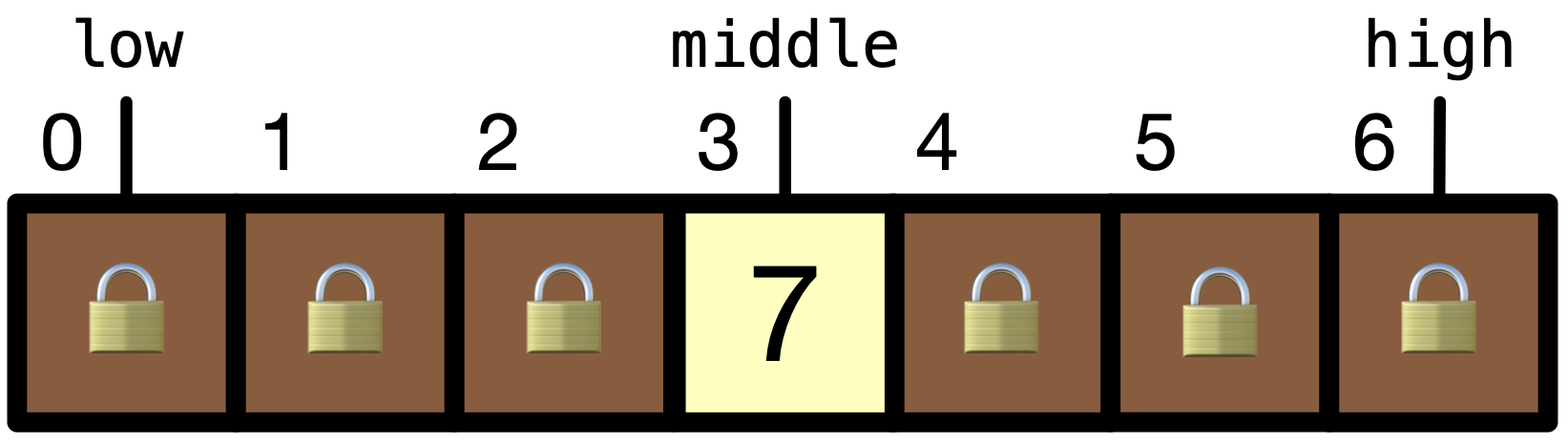
Since the value at index
middleis not equal toitem, which is9, we need to continue looking foritem. We can check iflist[middle] < item. If it is, we can discard the first half of the list. If it is not, we can discard the second half of the list. In our case,list[middle]is 7, which is less thanitem, which is9. Therefore, we can discard the first half of the list. We can do this by settinglow = middle + 1.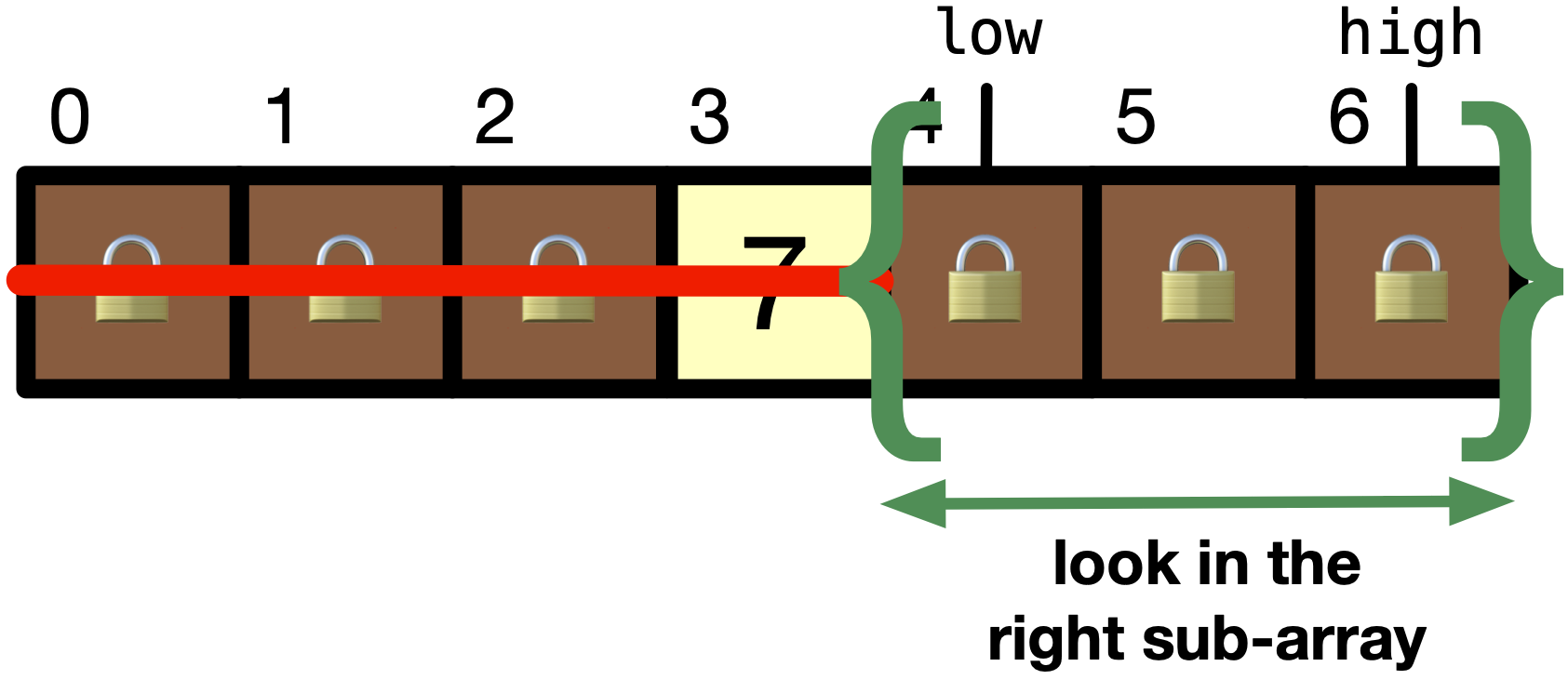
We can repeat step \(1\) and \(2\) but on the smaller right sub-array until we find
item. In our case,lowis4andhighis6. This makesmiddle = 5. Sincelist[middle]is10, which is less thanitem, which is9, next we can discard the second half of the sub-array (after middle).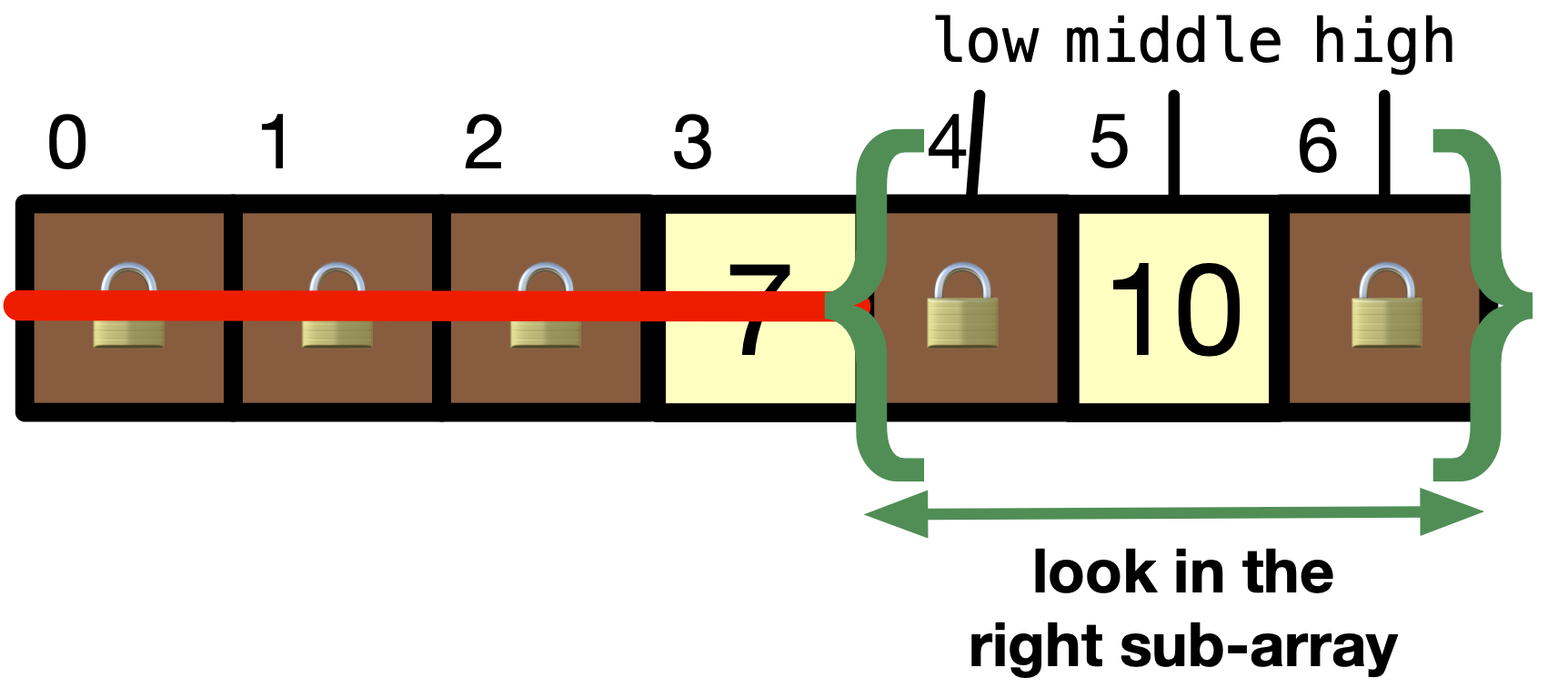
We can discard the second half of the sub-array by setting
high = middle - 1. After discarding the second half of the array, we havelow = 4andhigh = 4. This makesmiddle = 4.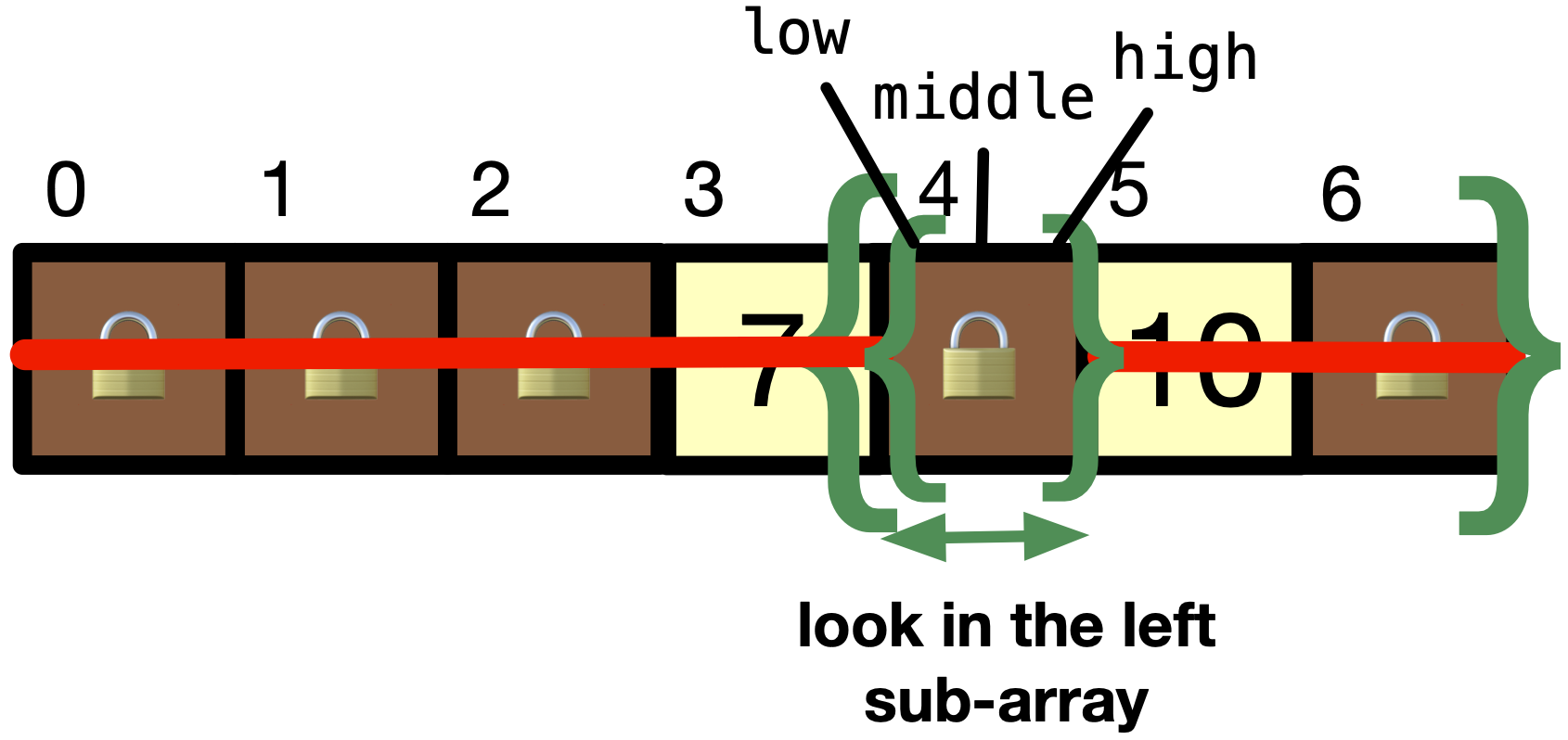
Since
list[middle]is9, which is equal toitem, we have founditemin the array.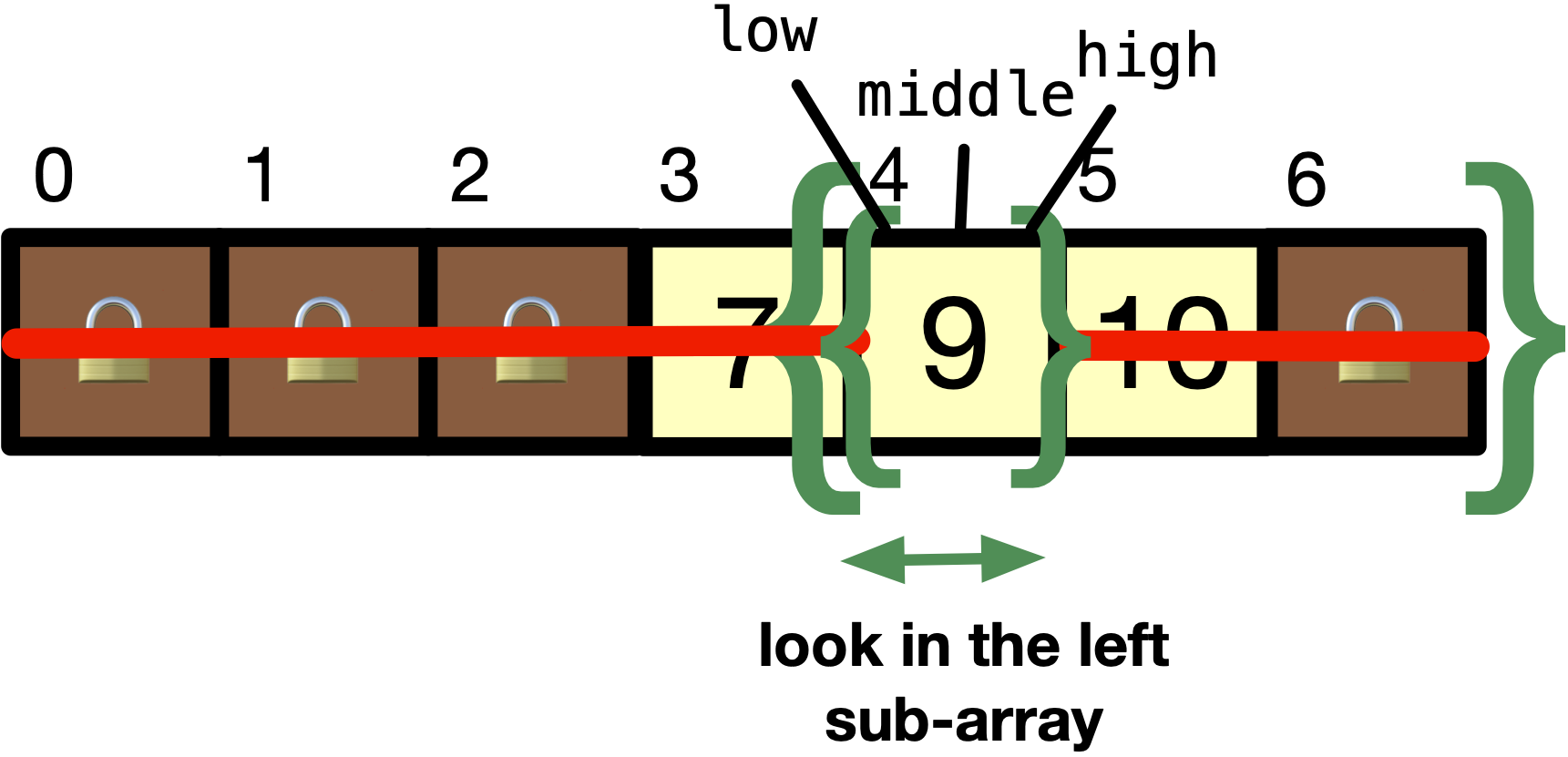
When not found!
If item in our example was 8, we would NOT have found it at index 4. However, the algorithm will continue with setting high = middle - 1. This would make high = 3, and low remains 4. The algorithm should terminate when low > high. This means that the algorithm has searched the entire array and has not found item.
15.2.1. Pseudocode#
To highlight the main steps of binary search, we can write the algorithm in pseudocode as follows:
Set
low = 0andhighto the length of the array - 1.Look at the element at index
middle = (low + high)/2.If the element at index
middleis equal toitem, returnmiddle.If the element at index
middleis less thanitem, theitemcould be in the right sub-array. Setlow = middle + 1to look at the right sub-array and go to step \(2\).Otherwise, set
high = middle - 1to look at the left sub array and go to step \(2\).If
low > high, return-1to indicate thatitemwas not found.
15.2.2. Implementation#
To implement binary search, we need to write a function that takes in an array, size of the array and an item to search for. The function should return the index of the item if it is found in the array. If the item is not found, the function should return -1. Download the following code binary-search.c if you want to play with it.
Code
#include <stdio.h>
int binarySearch(int list[], int listLength, int item) { int low = 0; int high = listLength - 1; int middle;
while (low <= high) { middle = (low + high) / 2; if (item == list[middle]) return middle; else if (item < list[middle]) high = middle - 1; else low = middle + 1; } return -1; }
int main() { int list[] = {1, 3, 5, 7, 9, 10, 12}; printf("Found 9 at index %d\n", binarySearch(list, 7, 9)); return 0; }
In line \(17\), we have exited from the while loop. This means that we have searched the entire array and have not found item. Therefore, we return -1 to indicate that item was not found.
15.2.3. Recursive Implementation#
We can also implement binary search recursively.
Thinking recursively, as we discussed in Section 11.2.1, requires us to think about a smaller problem. In the case of binary search, we can think about the smaller problem of searching a smaller sub-array. This would be our recursive case. Our base/terminating case is when we have searched the entire array and have or have not found item.
How would we reduce the size of the array from one function call to the next recursive function call? We did a similar thing when we implemented isPalindrome function recursively inSection 11.3.2. The idea is to communicate with the next recursive function call the new limits of the array, i.e. the values of low and high.
Similarly, in our recursive binary search implementation below, we pass the values of low and high to the next recursive function call. We can do so by passing the values of low and high as arguments to the recursive function call.
Code
1int binarySearchHelper(int list[], int low, int high, int item) {
2 if (high < low) // failure - item not in list
3 return -1;
4
5 int middle = (low + high) / 2;
6 if (item == list[middle]) // success
7 return middle;
8
9 else if (item < list[middle]) // try bottom half
10 return binarySearchHelper(list, low, middle - 1, item);
11
12 else // try top half
13 return binarySearchHelper(list, middle + 1, high, item);
14}
In line \(1\), we pass the array list, the values of low and high and the item to search for as arguments to the recursive function call. Initially, we can call the function to set low to 0 and high to the length of the array - 1.
Lines \(2\)–\(3\) handle the base case. If high is less than low, we have searched the entire array and have not found item. Therefore, we return -1 to indicate that item was not found.
Lines \(6\)–\(7\) handle another base case when we found item in the array. If item is equal to list[middle], we return middle to indicate that we have found item in the array.
Lines \(9\)–\(10\) handle the recursive case when item is less than list[middle]. In this case, we can discard the second half of the array by setting high = middle - 1 to the next recursive call. We can then call the recursive function to search the left sub-array by binarySearchHelper(list, low, middle - 1, item). The return before the recursive function call is important. This ensures that the value returned by the recursive function call is returned by the function. You can drop the return statement if it was a void function, but since it should return an int, we need to return the value returned by the recursive function call.
Lines \(12\)–\(13\) handle the recursive case when item is greater than list[middle]. In this case, we can discard the first half of the array by setting low = middle + 1 to the next recursive call. We can then call the recursive function to search the right sub-array by binarySearchHelper(list, middle + 1, high, item).
We can see that the values of low and high are updated in the recursive function call. This is how we reduce the size of the array from one function call to the next recursive function call.
Reduce number of arguments I would like to point out that functions with several arguments passed is not ideal, as someone may forget how to call the recursive function. We can improve this! We can implement a function that takes three arguments, an array, the size of the array and an item to search for. The function can then call the recursive function with the values of low and high set to 0 and the length of the array - 1, respectively. This is what we do in the following implementation. Download the following code binary-search-recursive.c if you want to play with it.
Code
#include <stdio.h>
int binarySearchHelper(int list[], int low, int high, int item); int binarySearchRecursive(int list[], int listLength, int item);
int main(){ int list[] = {1, 3, 5, 7, 9, 10, 12}; printf("Found 9 in index %d", binarySearchRecursive(list, 7, 9)); return 0; }
int binarySearchRecursive(int list[], int listLength, int item) { return binarySearchHelper(list, 0, listLength - 1, item); }
int binarySearchHelper(int list[], int low, int high, int item) { if (high < low) // failure - item not in list return -1;
int middle = (low + high) / 2; if (item == list[middle]) // success return middle; else if (item < list[middle]) // try bottom half return binarySearchHelper(list, low, middle - 1, item); else // try top half return binarySearchHelper(list, middle + 1, high, item); }
In lines \(12\)–\(14\), we call the recursive function binarySearchHelper with the values of low and high set to 0 and the length of the array - 1, respectively. As a developer, you can later just sell this function to your users, and they can call it with just three arguments, an array, size of the array and an item to search for. The function will then call the recursive function with the values of low and high set to 0 and the length of the array - 1, respectively.
Quiz
0 Questions
