Recursion in Patterns
Contents
11.2. Recursion in Patterns#
In the previous section, we discuss recursion in functions, e.g. greatest common divisor using euclidean algorithm or the factorial function. In this section, we discuss recursion in patterns.
In general, recursive functions will have the following structure:
Recursive function (problem)
if terminating condition
may do a simple calculation;
return;
else:
break problem into a smaller piece/s
Recursive function (smaller piece/s)
11.2.1. Print a row of stars#
Let’s start with a simple example. We want to print a row of stars recursively. The number of stars in the row is given as an input to the function. Since the function only prints, it does not return any values to the calling function. The function prototype is as follows:
void printRow(int n);
Think recursively! We need to “think recursively” to develop a recursive function. This means we need to think of doing a small task in printing the row, then calling the same function, but on a smaller row, for example. We can print one star then, call printRow(n - 1);. However, we need to remember this is only the recursive call. The terminating case could be the smallest possible row of stars, for example, a row of one star. Given that, the base case is when n == 0. In this case, we print *\n only. The following figure illustrates the recursive thought process.
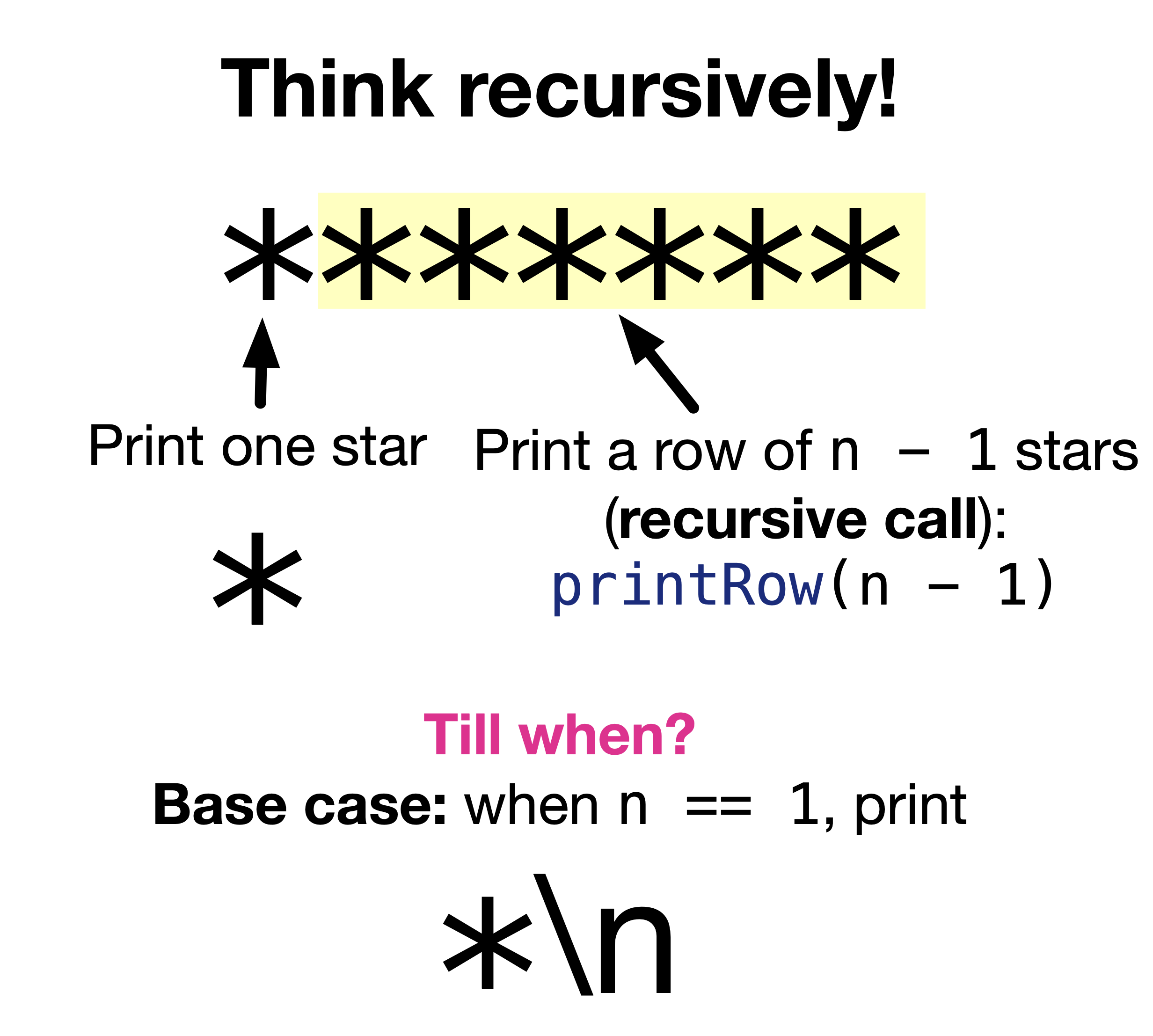
Fig. 11.5 Print a row of stars recursively.#
The following code uses the recursive function printRow. Download printRow.c if you want to run the program yourself.
Code
#include <stdio.h>
void printRow(int n);
int main(void) { int stars; printf("Enter number of stars:"); scanf("%d", &stars); printRow(stars); return 0; }
void printRow(int n) { if (n == 1) { printf("*\n"); } else { printf("*"); printRow(n - 1); } }
Line \(15\) will be executed only once in the base case, when n == 1.
Lines \(17\) to \(18\) will be executed several times as they are part of the recursive call till n == 1.
What happens when printRow(4) is called? Let’s trace printRow(4). In Fig. 11.6, we show the order of execution.
printRow(4)is called inmain.n == 4is not equal to1, so line \(12\) is executed.printRow(3)is called on line \(13\)n == 3is not equal to1, so line \(12\) is executed.printRow(2)is called on line \(13\)n == 2is not equal to1, so line \(12\) is executed.printRow(1)is called on line \(13\)n == 1is equal to1, so line \(10\) is executed.printRow(1)should return toprintRow(2)at line \(13\) when it was called, but there is no more code to execute inprintRow(2), soprintRow(2)should return toprintRow(3), and so on.
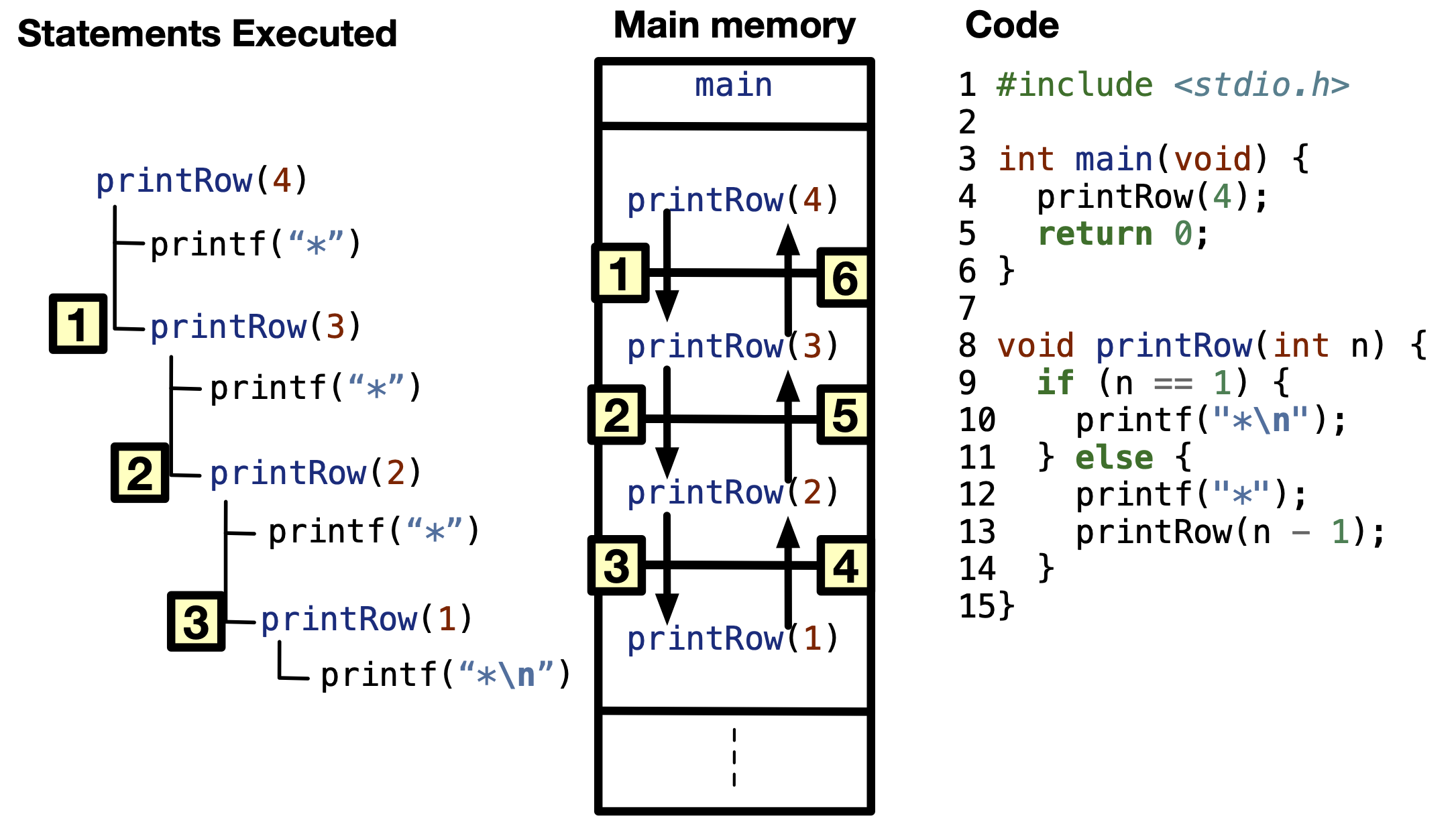
Fig. 11.6 The order of execution of printRow(4).#
What if we switch the order of printf(“*”) and printRow(n - 1)?
If we switch the order of printf("*") and printRow(n - 1) as in the following code, the order of execution of print statements will be different.
Code
#include <stdio.h>
void printRow(int n);
int main(void) { int stars; printf("Enter number of stars:"); scanf("%d", &stars); printRow(stars); return 0; }
void printRow(int n) { if (n == 1) { printf("*\n"); } else { printRow(n - 1); printf("*"); } }
In Fig. 11.7, we show the order of execution when the order of printf("*") and printRow(n - 1) is switched. In this case, the recursive call printRow(n - 1) is executed for all n first, then the printf("*") statements will be executed. This will make the first executed printf statement to be the one in the base case, and the last print statement to be the one in the recursive call with largest n.
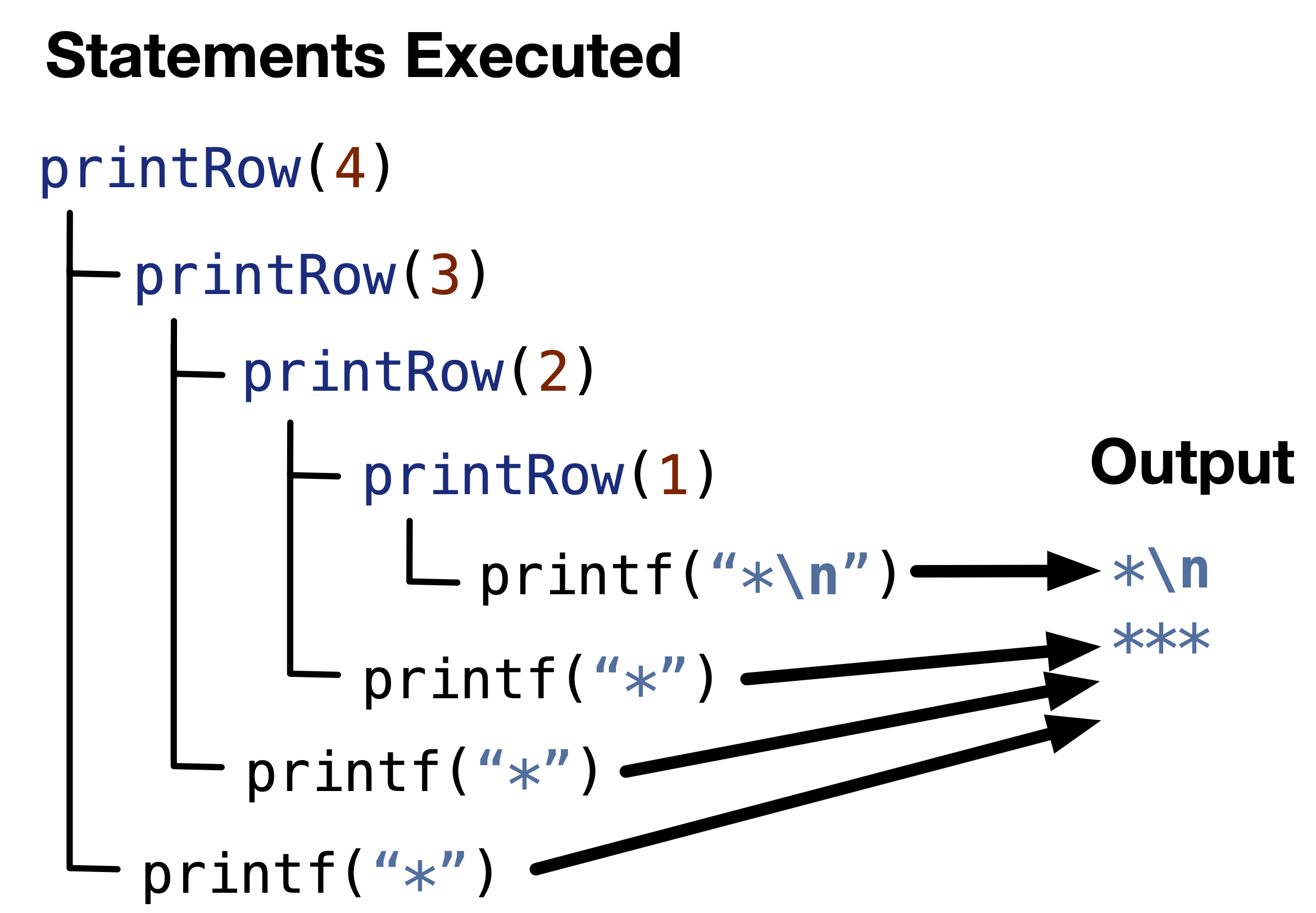
Fig. 11.7 The order of execution of printRow(4) when the order of printf("*") and printRow(n - 1) is switched.#
11.2.2. Print a triangle of stars#
Let’s take one more advanced step. We want to print a triangle of stars, as shown below, recursively.
***** **** *** ** *
The number of rows in the triangle is given as an input to the recursive function. Since the function only prints, it does not return any values to the calling function. The function prototype is as follows:
void printTriangle(int n);
Think recursively! We need to “think recursively” to develop a recursive function. This means we need to think of doing a small task in printing the triangle, then calling the same function, but on a smaller triangle, for example. We can print a row of stars then, call printTriangle(n - 1);. However, we need to remember this is only the recursive call. The terminating case could be the smallest possible triangle, for example, a triangle with one row. Given that, the base case is when n == 1. In this case, we print *\n only. The following figure illustrates the recursive thought process.
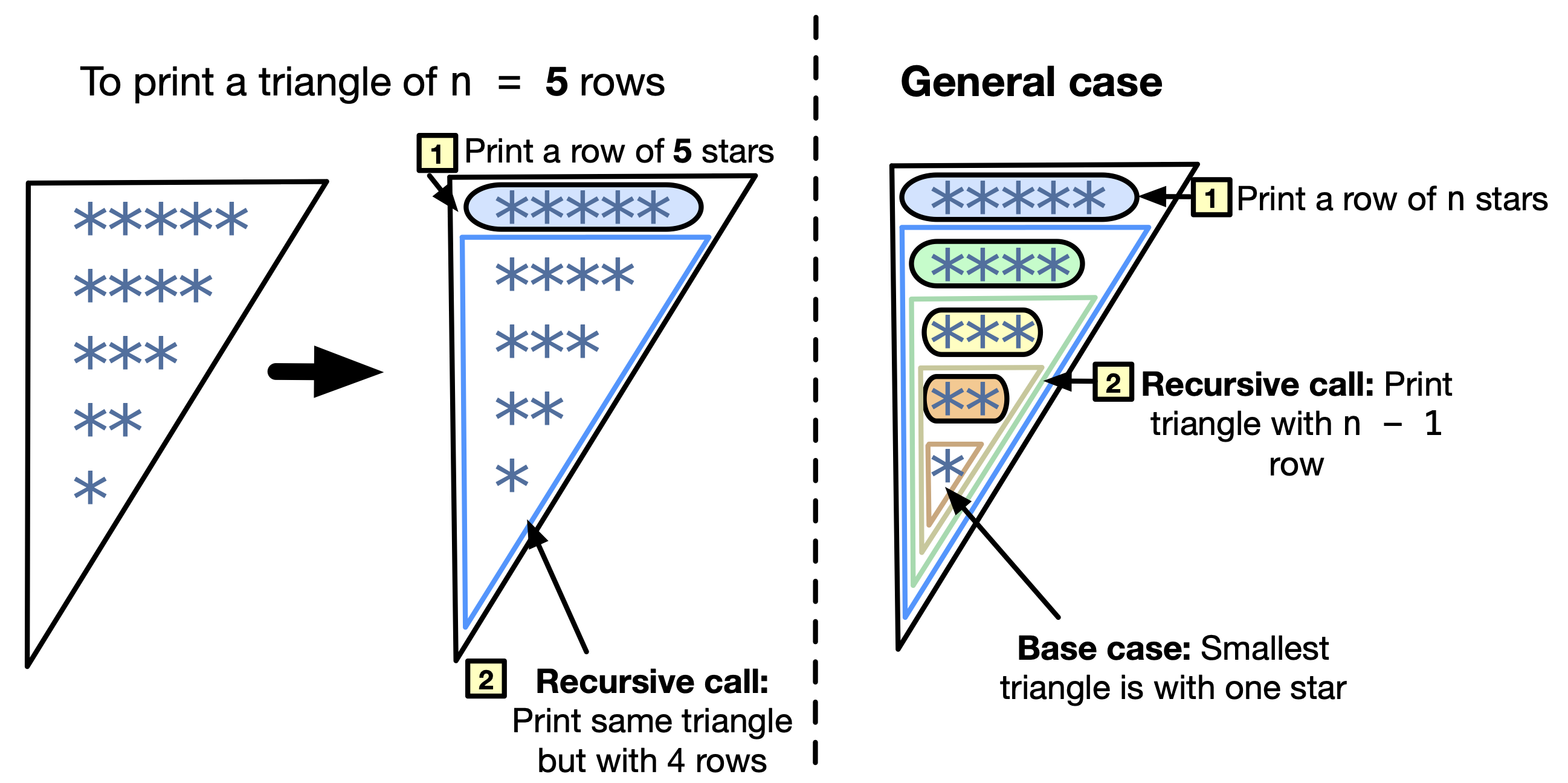
Fig. 11.8 Thinking recursively to print a triangle of stars.#
The following code snippet is one way to implement the recursive function printTriangle. The function printRow is the same as the one we used in the previous section. Here, if n == 1, we print 1 star and return. If n > 1, we print a row of stars, then call printTriangle(n - 1). If n < 1, we do nothing.
Code snippet
void printTriangle(int n) {
if (n == 1) {
printRow(n);
} else if (n > 1) {
printRow(n);
printTriangle(n - 1);
}
}
The following code shows another way to implement the recursive function printTriangle. The function printRow is the same as the one we used in the previous section. Here, if n > 0, we print a row of n starts using printRow(n) and call printTriangle(n - 1). If n was exactly 0, we print a 1 star using printRow(1), then call printTriangle(0). If n <= 0, we do nothing. Hence, technically, when n == 1, we only print one star. The base case is n <= 0.
Download printTriangle.c if you want to run the program yourself.
Code
#include <stdio.h>
void printRow(int n); void printTriangle(int n);
int main(void) { int rows; printf("Enter number of rows:"); scanf("%d", &rows); printTriangle(rows); return 0; }
void printTriangle(int n) { if (n > 0) { printRow(n); printTriangle(n - 1); } }
void printRow(int n) { if (n == 1) { printf("*\n"); } else { printf("*"); printRow(n - 1); } }
The following figure shows the order of execution of printTriangle(4).

Fig. 11.9 Tracing print triangle function with n = 4: printTriangle(4).#
11.2.3. Print an inverted triangle of stars#
What should we do differently to implement a recursive function that prints the same triangle we printed before but inverted? The triangle we want to print is as follows:
* ** *** **** *****
The following figure illustrates the recursive thought process. We understand from the following figure that we should first print a smaller sized triangle, then print a row of n stars. This is reversed order of steps compared to Fig. 11.8, where we first printed a row of stars then a triangle of smaller size.
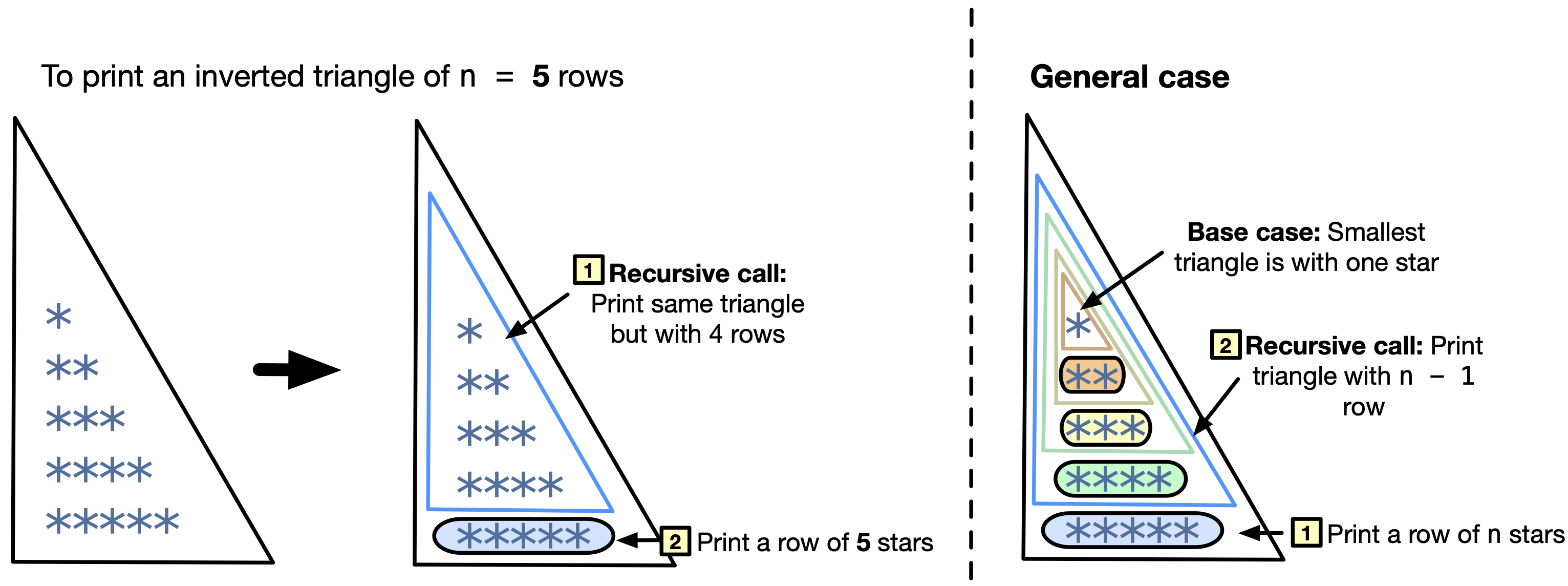
Fig. 11.10 Thinking recursively to print an inverted triangle of stars.#
The following code snippet is one way to implement the recursive function printInvertedTriangle. The function printRow is the same as the one we used in the previous section. Download printInvertedTriangle.c if you want to run the program yourself.
Code
#include <stdio.h>
void printRow(int n); void printInvertedTriangle(int n);
int main(void) { int rows; printf("Enter number of rows:"); scanf("%d", &rows); printInvertedTriangle(rows); return 0; }
void printInvertedTriangle(int n) { if (n > 0) { printInvertedTriangle(n - 1); printRow(n); } }
void printRow(int n) { if (n == 1) { printf("*\n"); } else { printf("*"); printRow(n - 1); } }
In the above code, notice that we switched the order of printRow(n) call and printInvertedTriangle(n - 1); call. This is because we want to print a smaller triangle first, then a row of stars. The following figure shows the order of execution of printInvertedTriangle(4). Remember that printInvertedTriangle(0) will not execute anything, since n is 0. Also, recall that calls to printRow function will recursively call printRow until n == 1, then print * and return as we discussed in Section 11.2.1.

Fig. 11.11 Tracing printInvertedTriangle function with n = 4: printInvertedTriangle(4).#
11.2.4. Print a pattern recursively#
One final advanced step in this section is to print the pattern of stars in the following figure recursively, given the maximum number of stars in a row n. For example, the following pattern has n = 5.
***** **** *** ** * ** *** **** *****
Since the function only prints, it does not return any values to the calling function. The function prototype is as follows:
void printPattern(int n);
Think recursively! We need to “think recursively” to develop a recursive function. This means to print a pattern, we need to think of doing a small task/s in addition to printing a smaller sized pattern. The following figure illustrates the recursive thought process. As shown, we can print a row of stars then, call printPattern(n - 1);, then print a row of stars again. However, we need to remember this is only the recursive call part of the function. The terminating case could be the smallest possible pattern, for example, a pattern with two rows of 1 star each enclosing no special pattern. Given that, the base case is when n <= 0. In this case, we print nothing.
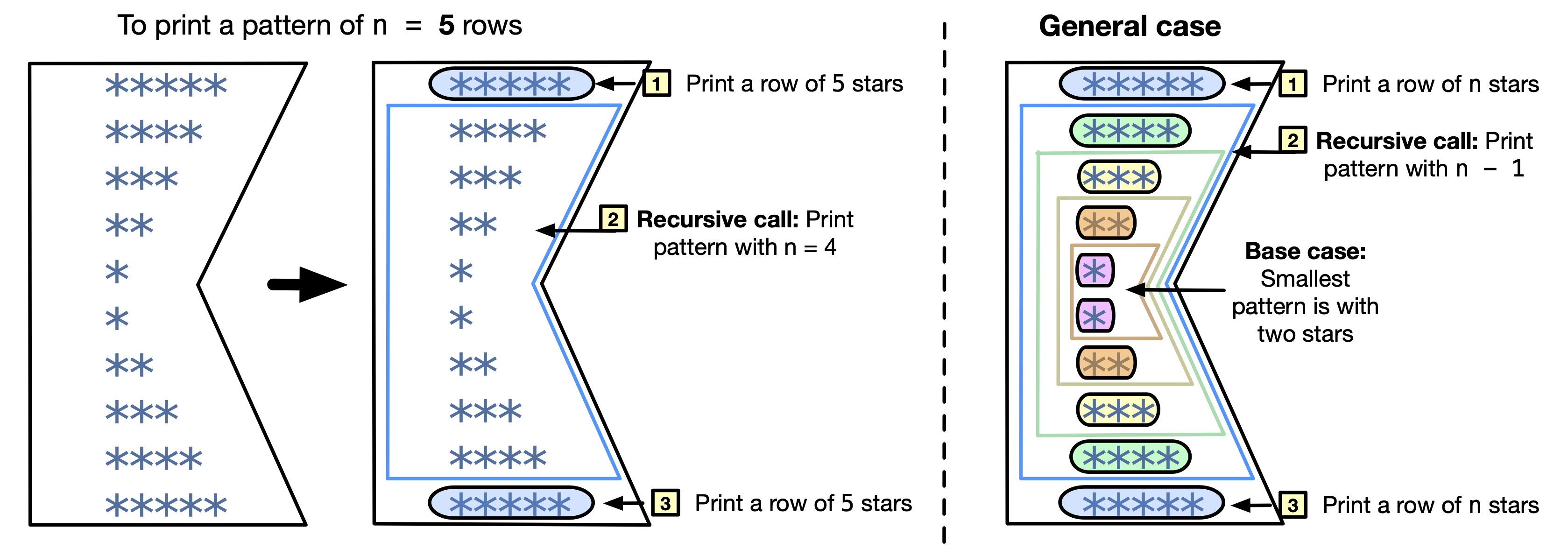
Fig. 11.12 Thinking recursively to print a pattern of stars.#
The following code is one way to implement the recursive function printPattern. The function printRow is the same as the one we used in the previous sections. Download printPattern.c
Code
#include <stdio.h>
void printRow(int n); void printPattern(int n);
int main(void) { int rows; printf("Enter number of max stars in a row:"); scanf("%d", &rows); printPattern(rows); return 0; }
void printPattern(int n) { if (n > 0) { printRow(n); printPattern(n - 1); printRow(n); } }
void printRow(int n) { if (n == 1) { printf("*\n"); } else { printf("*"); printRow(n - 1); } }
Notice that lines \(16\) – \(18\) is the same order of statements illustrated in Fig. 11.12.
The following figure shows the order of execution of printPattern(4). Remember that printPattern(0) will not execute anything, since n is 0. Also, recall that calls to printRow function will recursively call printRow until n == 1, then print * and return as we discussed in Section 11.2.1.
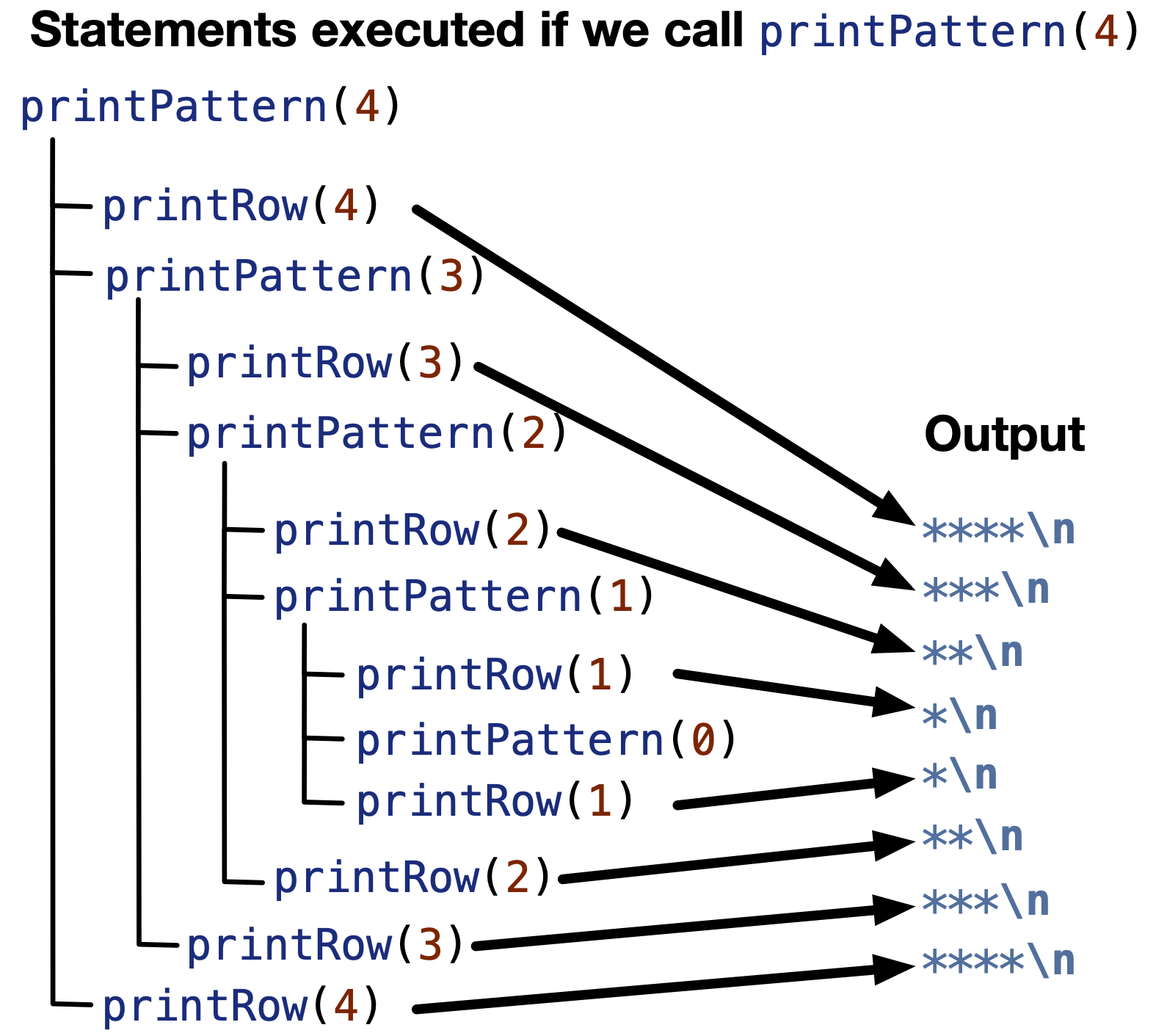
Fig. 11.13 Tracing printPattern function with n = 4: printPattern(4).#
Quiz
0 Questions
