14.1. Insertion Sort#

The first sorting algorithm we discuss is insertion sort. Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort. However, it is an excellent algorithm for learning about sorting and is often used to sort small lists or arrays.

14.1.1. Algorithm#

The general idea of insertion sort is to iterate through the array, and insert each element into its correct position with respect to the elements that have already been sorted. For example, if the only the first 3 elements of the array are sorted, the forth element will be inserted into its correct position with respect to the first 4 elements. This happens by by shifting all elements that are greater than the forth element to the right, and inserting A[top] in place of the left most element greater than forth element. This places the forth element in its correct position with respect to the first four elements.

Given the following example array named int A[] = {9, 2, 6, 5, 1, 7};

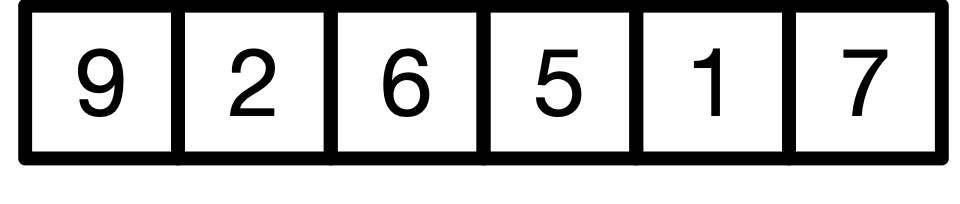
array-example

Insertion sort works as follows:

  1. Insert the second element into it’s correct position, with respect to the first two elements.

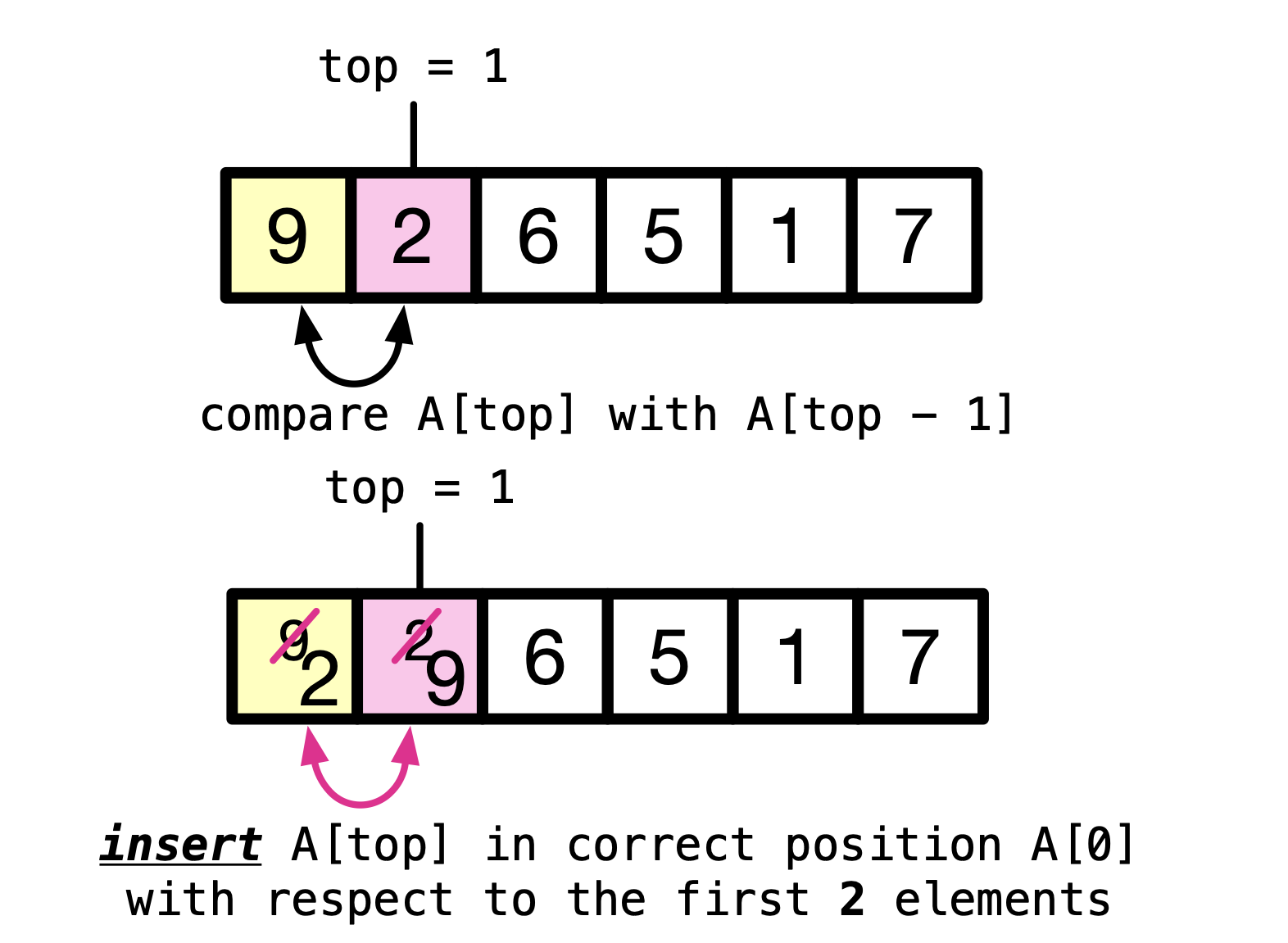
    first-two-elements-insert

    After the first iteration, the first two elements — as a sub-array — are sorted.

  2. Insert the third element into it’s correct position, with respect to the first three elements.

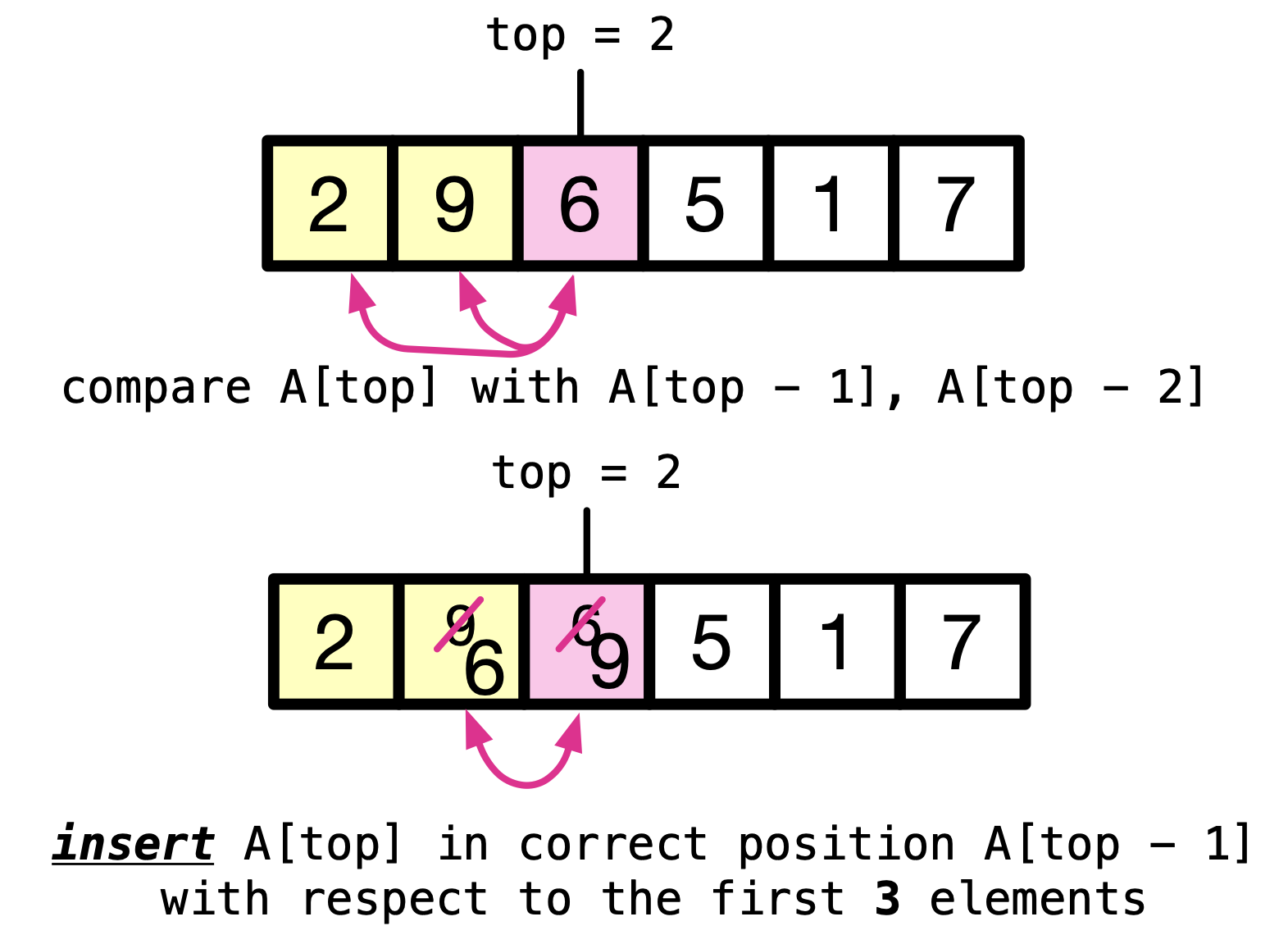
    first-three-elements-insert

    After the second iteration, the first three elements — as a sub-array — are sorted.

  3. Insert the fourth element into it’s correct position, with respect to the first four elements. This happens by shifting all elements that are greater than A[top] to the right, and insert A[top] in its correct position with respect to the first 4 elements.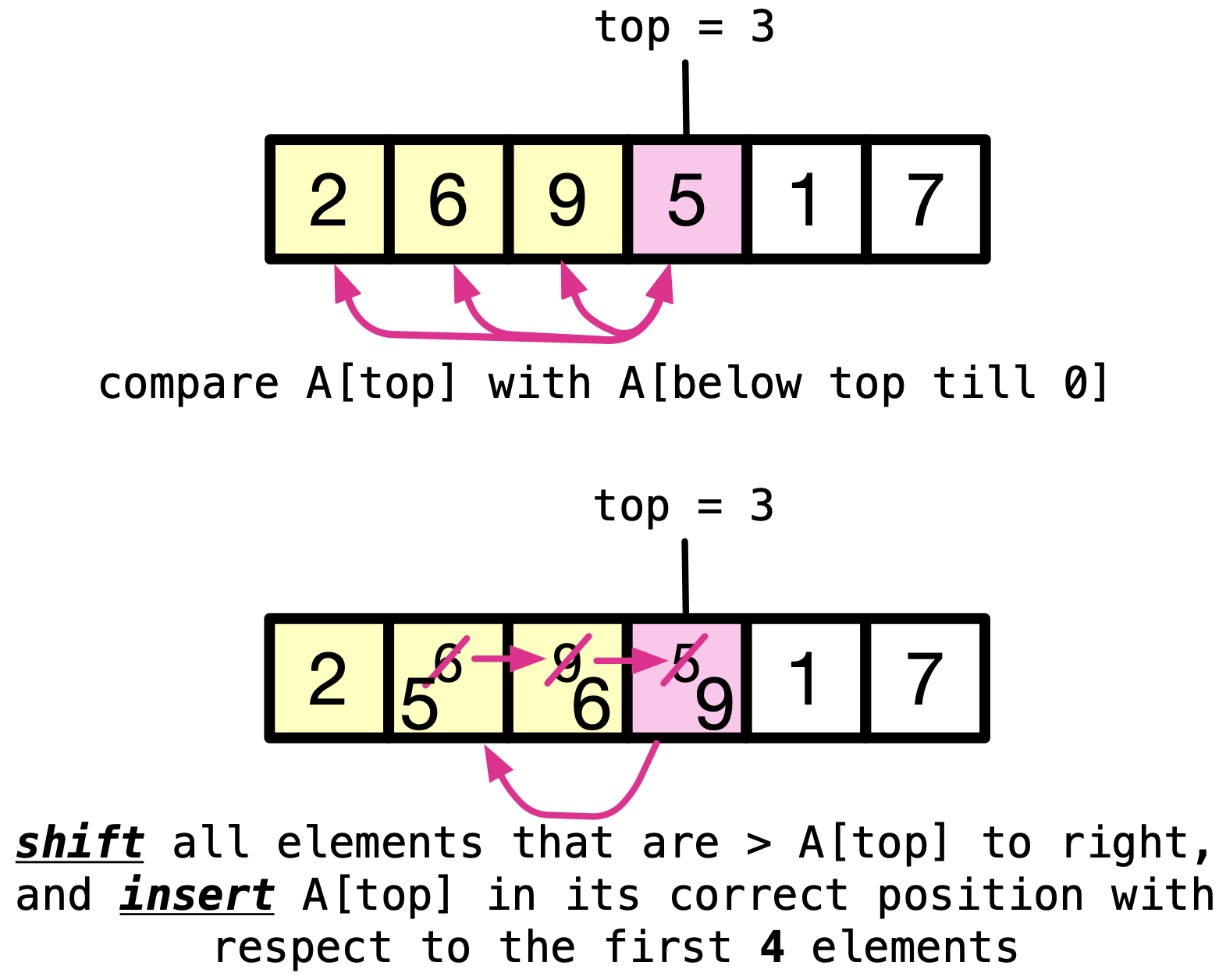

    first-four-elements-insert

    After the third iteration, the first four elements — as a sub-array — are sorted.

  4. Insert the fifth element into it’s correct position, with respect to the first five elements by shifting all elements that are greater than A[top] to the right, and inserting A[top] in place of the left most element greater than A[top]. This places A[top] in its correct position with respect to the first 5 elements.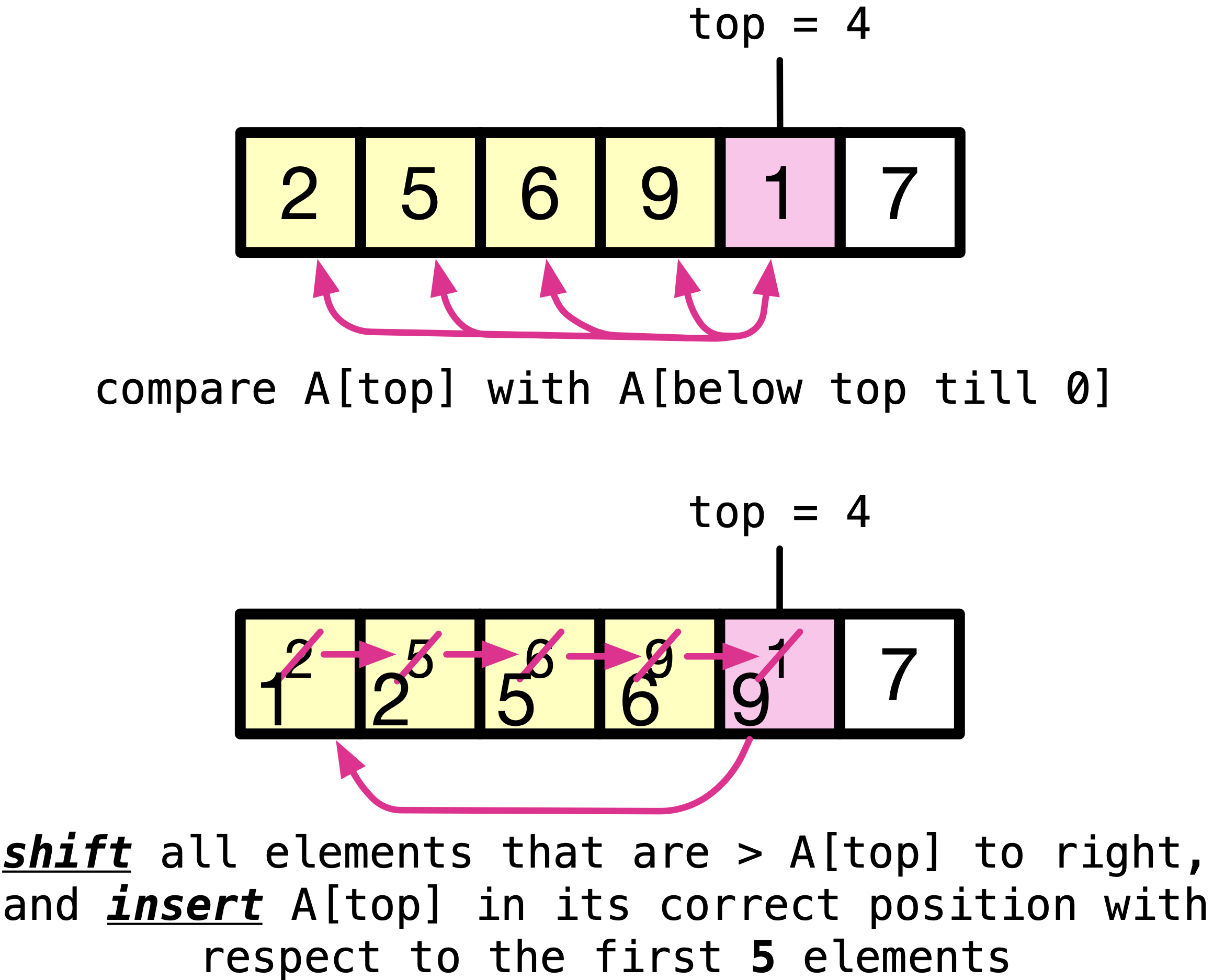

    first-five-elements-insert

    After the fourth iteration, the first five elements — as a sub-array — are sorted.

  5. Do the same as step 4, but with the sixth element.

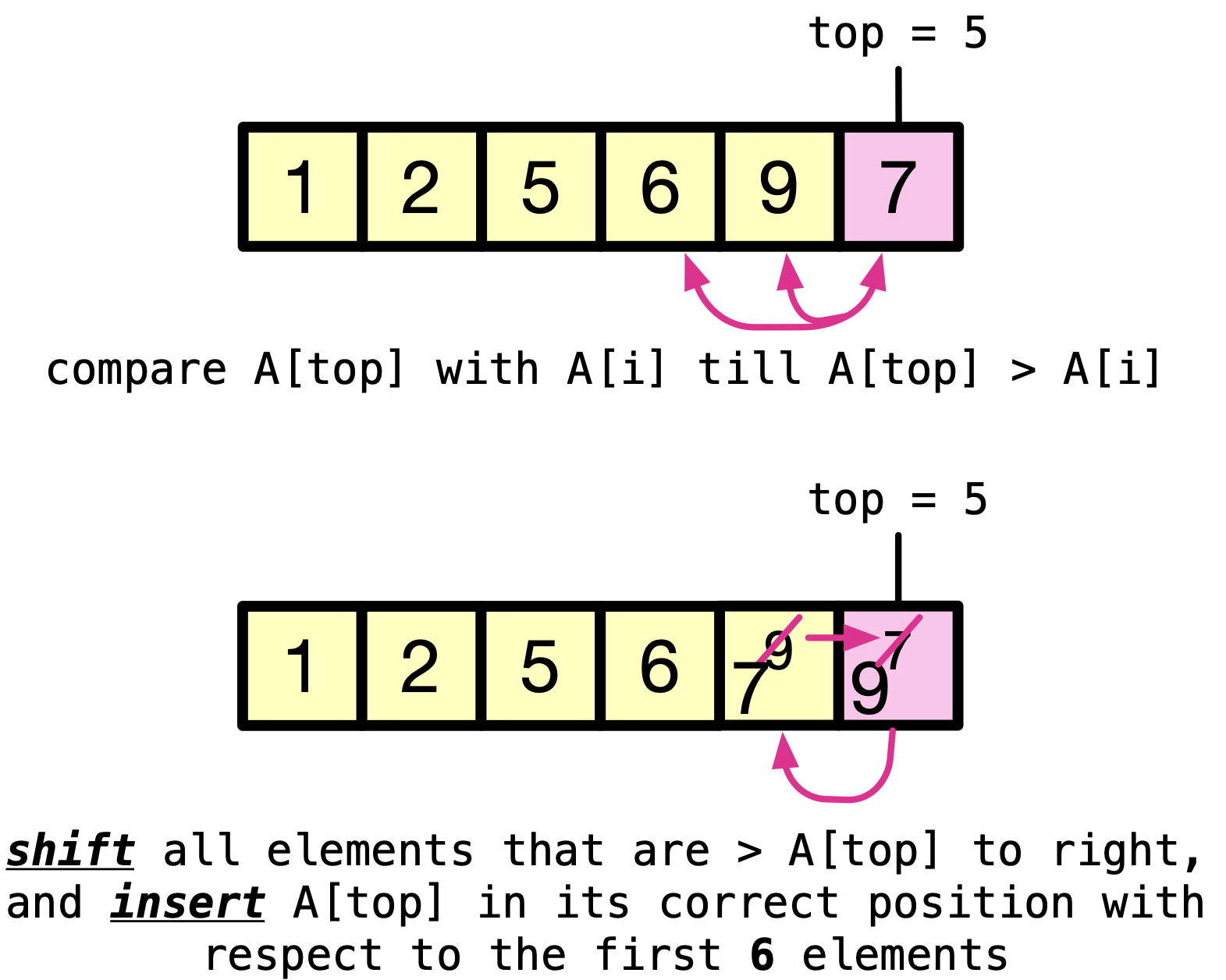
    first-six-elements-insert

    After the fifth iteration, the first six elements — as a sub-array — are sorted.

To implement insertion sort, we need to keep track of the index of the element that is currently being inserted into its correct position. This index is called top. We also need to keep track of the index of the element that is currently being compared to A[top]. This index is called ind. We also need to keep track of the value of A[top] so that we can insert it into its correct position. This value is called item.

14.1.2. Pseudocode#

We write pseudocode for insertion sort as follows:

  1. Set top to 1,

  2. Set item to A[top], and ind to top.

  3. If item is smaller than A[ind - 1], then set A[ind] to A[ind - 1] and decrement ind.

  4. Repeat 3 until ind is 0 or when item is no longer smaller than A[ind - 1]. This shifts all elements that are greater than item to the right.

  5. Now, chose the correct position for item by setting A[ind] to item.

  6. In the next iteration, set top to top + 1, set item to A[top], and ind to top.

  7. Repeat 3-6 until top is equal to listLength.

14.1.3. Implementation#

The following code snippet shows the insertion sort function.

Code 


#include <stdio.h>
void printArray(int list[], int listLength) {
  for (int i = 0; i < listLength; i++) {
    printf("%d ", list[i]);
  }
  printf("\n");
}


void insertionSort(int A[], int listLength) {
  int top;


  for (top = 1; top < listLength; top++) {
    int item = A[top];
    int ind = top;


    while (ind > 0 && item < A[ind - 1]) {
      // shift all elements > item to the right
      A[ind] = A[ind - 1];  
      ind--;
    }


    A[ind] = item;
    printf("After iteration %d: ", top);
    printArray(A, listLength);
  }
}


int main(void) {
  int list[] = {9, 2, 6, 5, 1, 7};


  insertionSort(list, 6);
  printArray(list, 6);


  return 0;
}

Quiz

0 Questions

X