Recursive functions by definition
Contents
11.1. Recursive functions by definition#
Recursion is a method of solving a problem that requires first solving smaller instances of the same problem. In programming, recursion is when a function calls itself but on a smaller problem/input. The function calls itself repeatedly until a solution is found on the smallest problem, which is when the function returns a solution and stops calling itself.
11.1.1. Euclidean Algorithm for Fining Greatest Common Divisor#
There are problems that have a solution defined recursively. For example, the Euclidean algorithm for finding the greatest common divisor (GCD) of two numbers is defined recursively. The Euclidean algorithm is a method for finding the greatest common divisor of two numbers. The algorithm is based on the following observation: if a and b are two positive integers, then the greatest common divisor of a and b is the same as the greatest common divisor of a and a - b, if a > b.
Hence, the algorithm is as follows:
If
a > b, then the greatest common divisor (GCD) ofaandbis the GCD ofa - banda.If
aandbare equal, then the greatest common divisor ofaandbisa(orb).
Mathematically, the Euclidean algorithm is defined as follows:
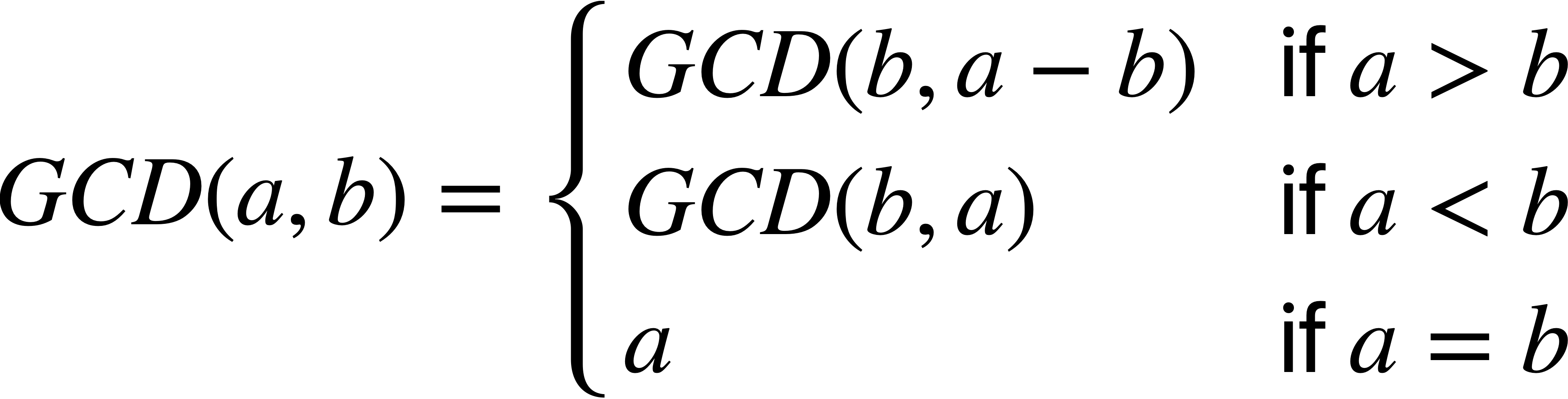
Fig. 11.1 GCD of two numbers is defined recursively.#
For example, the greatest common divisor of 20 and 8 is 4. To find the GCD using the formula above, \(GCD(20, 8)\) \(\rightarrow\) \(GCD(8, 20 - 8 = 12)\) \(\rightarrow\) \(GCD(12, 8)\) \(\rightarrow\) \(GCD(8, 12 - 8 = 4)\) \(\rightarrow\) \(GCD(4, 8 - 4 = 4) = 4\).
The Euclidean algorithm can be easily implemented recursively as follows. Download gcd.c if you want to run the program yourself.
Code
#include <stdio.h>
int gcd(int a, int b);
int main(void) { int gcdAnswer = gcd(20, 8); printf("gcd(20, 8) = %d\n", gcdAnswer); return 0; }
int gcd(int a, int b) { if (a == b) { return a; } else if (a > b) { return gcd(b, a - b); } else { return gcd(b, a); } }
What really happens when we call gcd function?
The following video explains what happens when we call the gcd function.
As the video discusses, recursive functions use up a lot of memory. This is because the function calls itself and the function call is stored in the stack. This happens repeated till a solution is found. The space allocation also takes time to complete. The main advantage of recursive functions is that they are easy to implement in cases where the mathematical formula is given, e.g. the Euclidean algorithm.
Given the disadvantages of recursive functions, it is important to know that we rarely use them in the real-world.
11.1.2. Factorial of a number#
Previously, we discussed the factorial of a number in Section 5.2.1. The factorial of a number is defined as follows:
We implemented an iterative function to calculate the factorial of a number using a for loop as follows:
Code
int factorial(int n) {
int fact = 1;
for (int i = 1; i <= n; i++) {
fact = fact * i;
}
return fact;
}
In the same function call, we repeatedly multiply the factorial by the next number till the number reaches n, and factorial is returned.
We can define the factorial of a number recursively. The factorial of a number is defined recursively as follows:
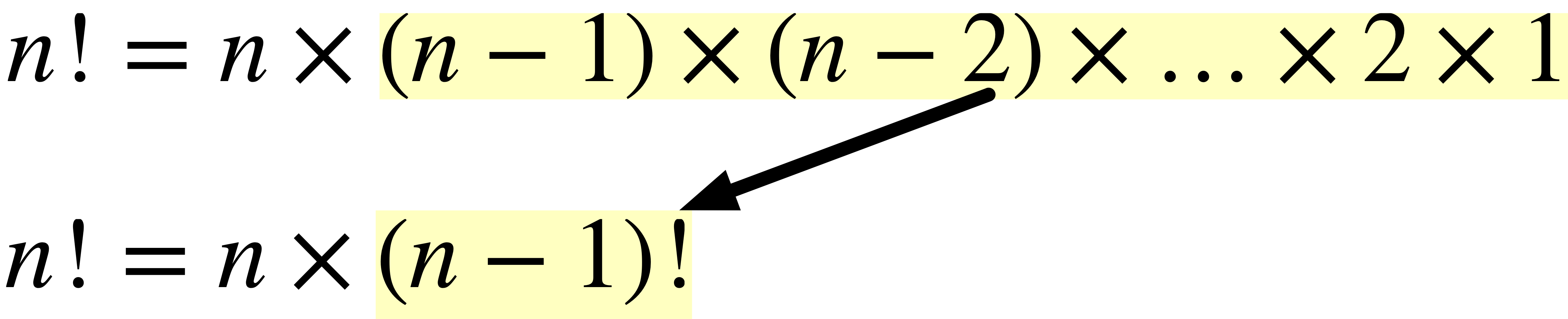
Fig. 11.2 Factorial of a number can be defined recursively.#
Given the mathematical definition, we can implement the factorial function recursively as follows:
Code [Errorneous]
int factorial(int n);
int main(void) { int fact = factorial(4); return 0; }
int factorial(int n) { return n * factorial(n - 1); }
The above code will not work. Why? In Fig. 11.3, we call the factorial function with n = 4, which calls the factorial with n = 3, then n = 2, then n = 1, then n = 1, then n = 0, then n = -1, and so on. The recursive call will never end. This is because the function does not have a base/terminating case. The smallest number of which the factorial is known is 0, and the factorial of 0 is 1. Hence, the function should return 1 when n = 0. This is the base or terminating case.

Fig. 11.3 A recursive factorial function without a base/terminating case can call itself infinitely, or till the space of the stack is exhausted.#
A corrected factorial function looks as follows, or you can download factorial-recursive.c to play with the code yourself.
Code [Correct]
#include <stdio.h>
int factorial(int n);
int main(void) { printf("4! = %d\n", factorial(4)); printf("1! = %d\n", factorial(1)); printf("0! = %d\n", factorial(0)); return 0; }
int factorial(int n) { if (n == 0) { return 1; } else { return n * factorial(n - 1); } }
In Fig. 11.4, we show the order of execution of the recursive function calls of the factorial function. The function returns a value to the previous function instance when it reaches the base case of n = 0.
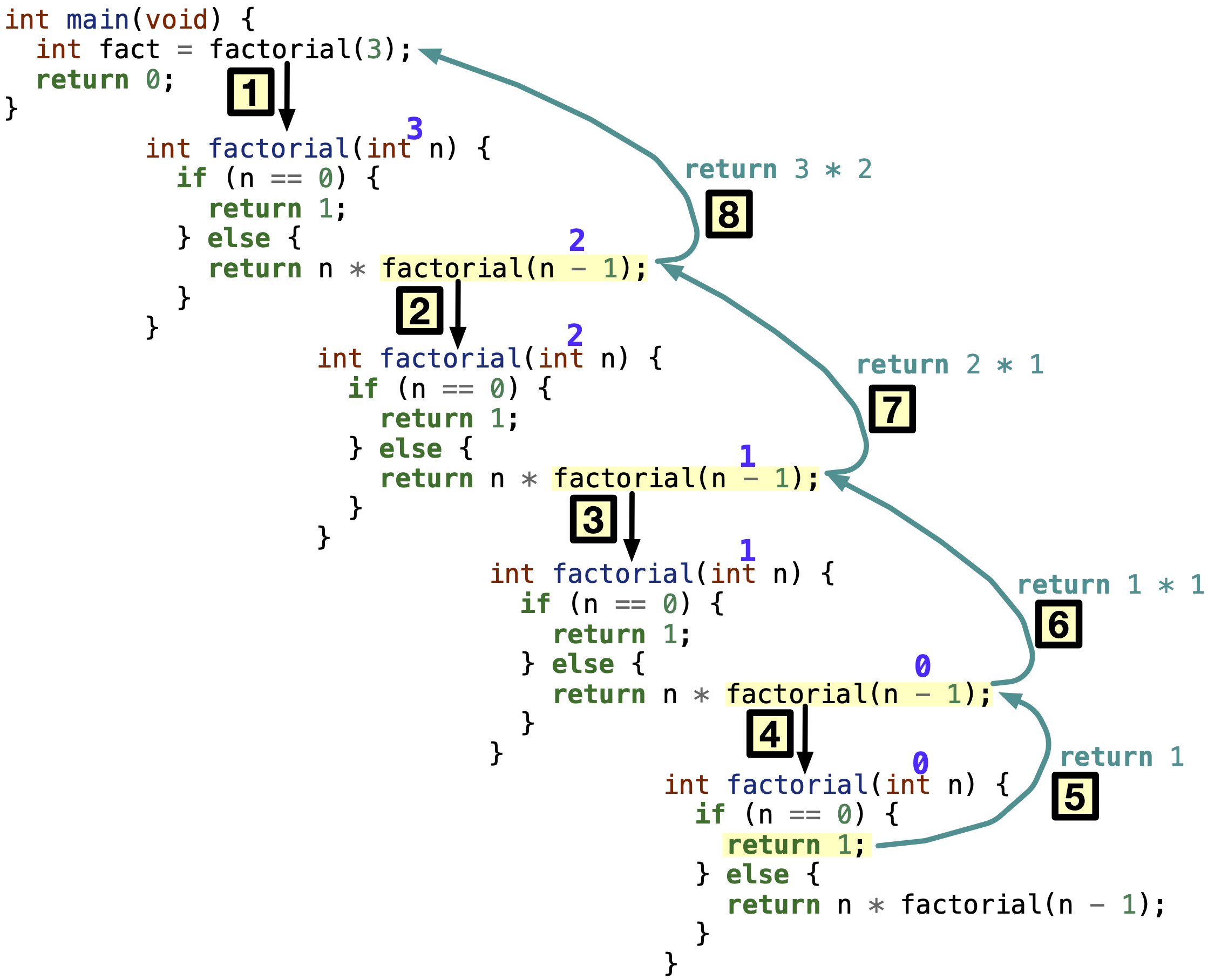
Fig. 11.4 A recursive factorial function with a base/terminating case will call itself until it reaches the end of the base case. This is when it will return a value to the previous function instance.#
Lesson learned. All recursive functions must have a base/terminating case, along with a recursive call, as illustrated in the figure below. Base case is when the function returns a value without calling itself, and it happens only when we reached the smallest problem that we have a solution to. Recursive call is when the function calls itself on a smaller problem than the original. Recursive calls should move closer to the base case with every call.

Quiz
0 Questions
