Why and how to use 2D arrays?
Contents
9.1. Why and how to use 2D arrays?#
Two-dimensional arrays are useful when information is better represented in form of rows and columns like a board in board games, pixel colors on a computer screen, database of course grades of all students, items on a shelf in the grocery store etc.
Similar to 1D arrays, it is powerful to represent all the rows and columns using a single variable/identifier.
9.1.1. How to create a 2D array?#
9.1.1.1. Declaration Only#
To only declare a 1D array, we define the number of elements it will hold, e.g., int myArray[6];. Similarly, to declare a 2D array, we need to define the number of rows and columns in the 2D array.
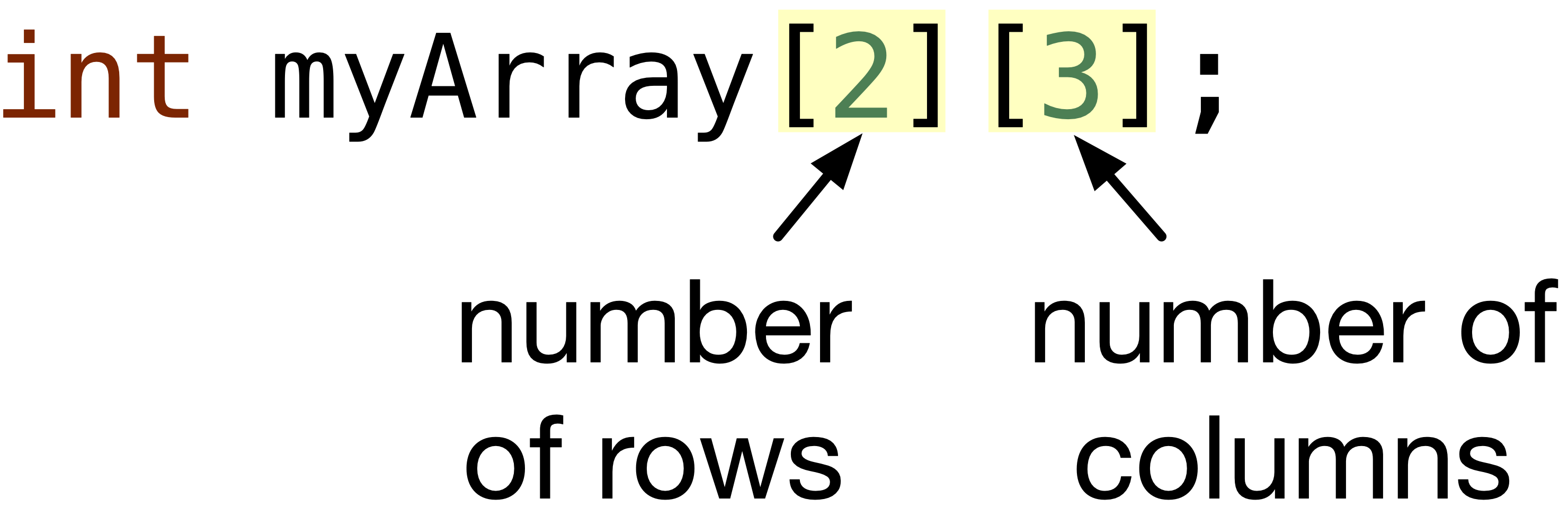
Fig. 9.1 Declaring a 2D array with elements of int type, identifier/variable name is myArray, number of rows is \(2\) and number of columns is \(3\).#
To access and initialize elements in the 2D array, we can do:
myArray[0][0] = 1;
myArray[0][1] = 2;
myArray[0][2] = 3;
myArray[1][0] = 4;
myArray[1][1] = 5;
myArray[1][2] = 6;
This would initialize a 2D array that looks like the following:
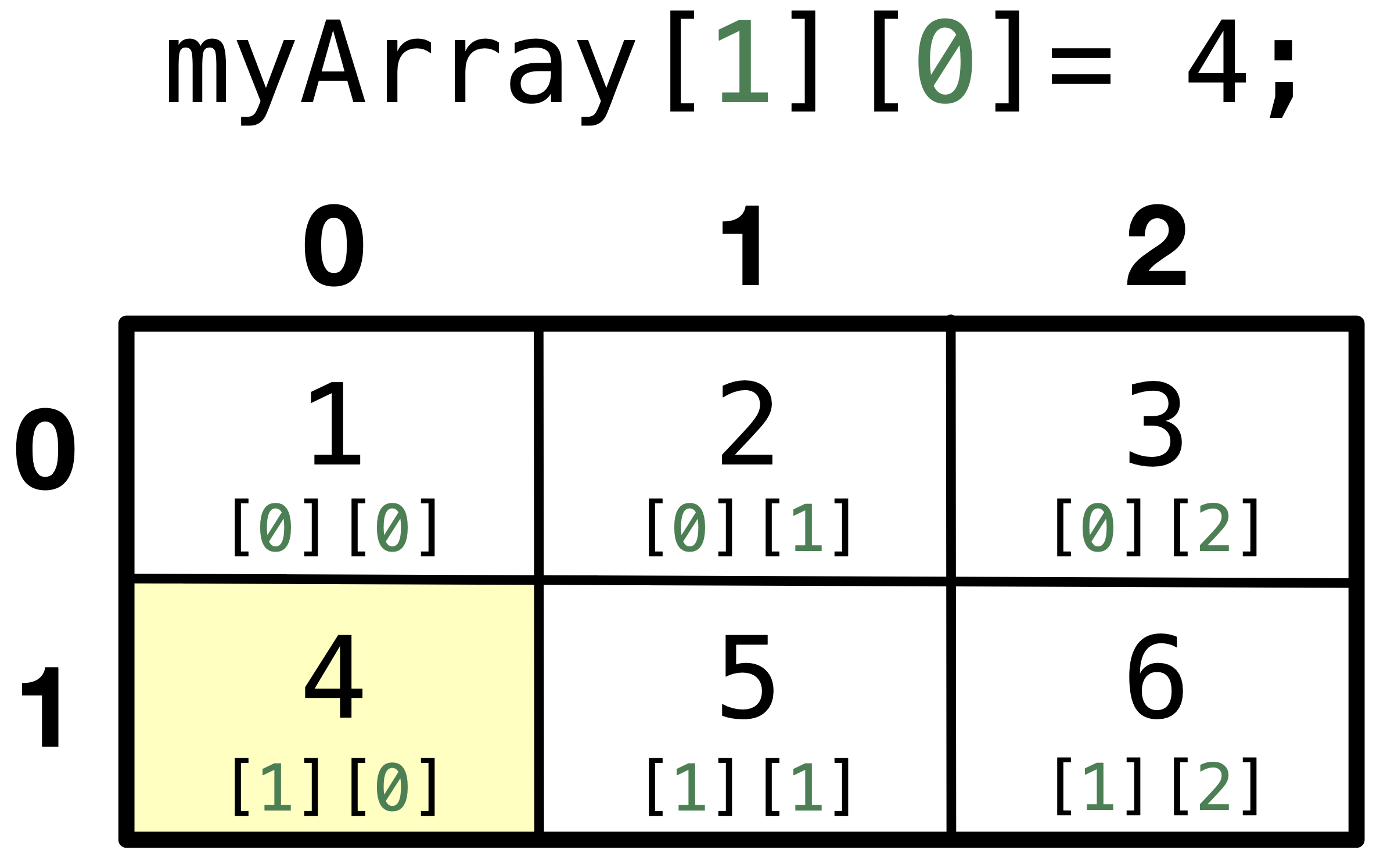
Fig. 9.2 The indexing of the rows and columns in a 2D array. Accessing myArray[1][0] = 4; will access the second row, and first column and assign 4 to it.#
You can initialize a 2D array using a nested for loop. The outer loop will be responsible for looping over the row index and the inner loop can loop over the column indices for each row. For example, in the following code we initialize a 2D array using a nested for loop. Download initialize-2d.c if you want to run the program yourself.
Code
#include <stdio.h>
int main(void) { int myArray[3][4];
for (int row = 0; row < 3; row++) { for (int col = 0; col < 4; col++) { myArray[row][col] = row * 4 + col; printf("myArray[%d][%d] = %d\n", row, col, myArray[row][col]); } } return 0; }
9.1.1.2. Declaration and Initialization#
1D arrays can be declared and initialized in the same statement by either defining or not defining the size of the array as follows.
int myArray[6] = {1, 2, 3, 4, 5, 6};int myArray[] = {1, 2, 3, 4, 5, 6};
On the other hand, we can declare and initialize the 2D array by defining the number of rows and columns, and enclosing each row and the entire array between curly brackets {} as follows:
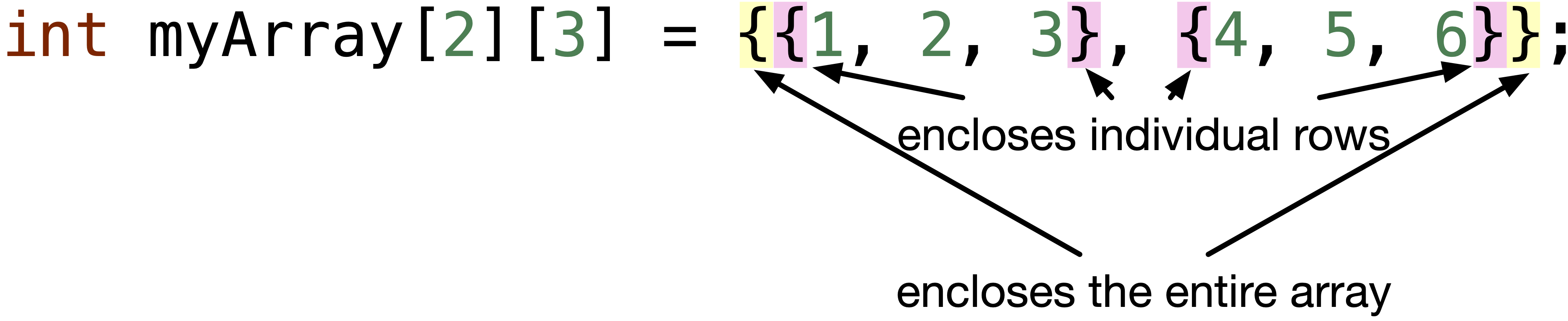
or without the {} that encloses each row,
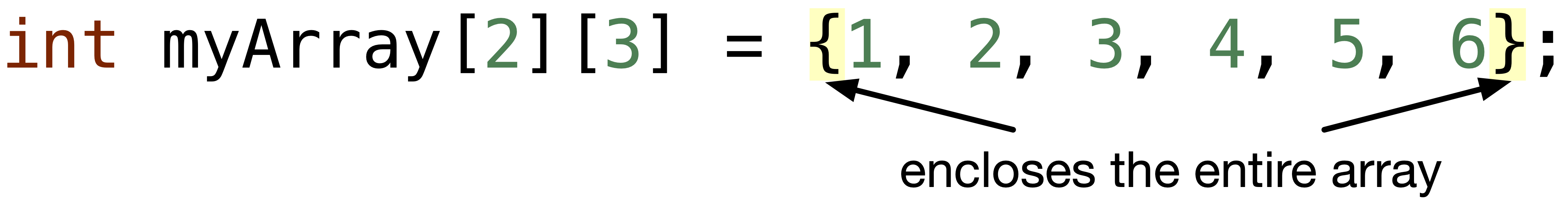
or without defining the number of rows.
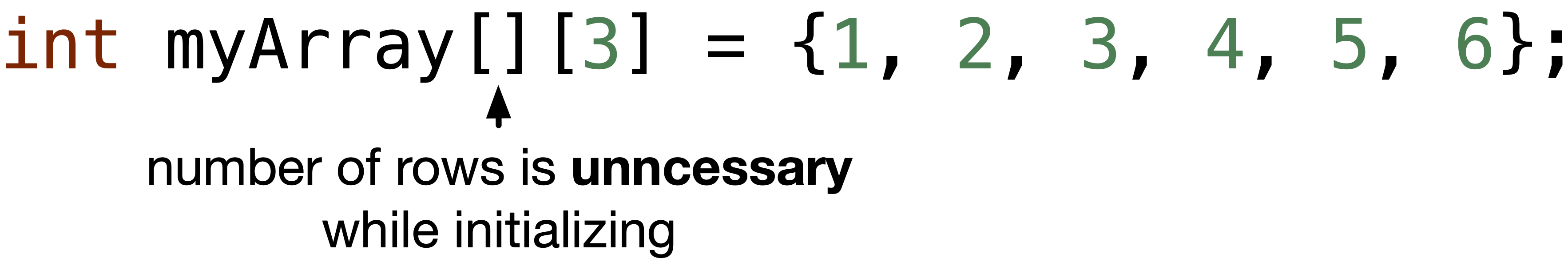
The number of rows is not required as the compiler will fill the array row by row, i.e. in “row major” order. For example, if the number of rows is unknown, the number of columns is \(3\), and the array is initialized with \(9\) elements, the first row will have 3 elements, the second row will have 3 elements and so on. Hence, the number of rows can be easily deduced if the number of columns and the elements are defined. To better understand “row major” order, let’s dive deeper into how a 2D array is stored in the main memory.
9.1.2. What does a 2D array look like in memory?#
The main memory is divided into cells. Each cell has an address, and it can store a byte. How is a 2D array stored in the 1D memory? Arrays are stored in “row major” order in the main memory. This means that the elements are stored row by row. For example, for
int myArray[][3] = {1, 2, 3, 4, 5, 6};
the elements in the memory are stored as shown in Fig. 9.3, where all elements in the first row appears first, then all elements in the next row and so on.
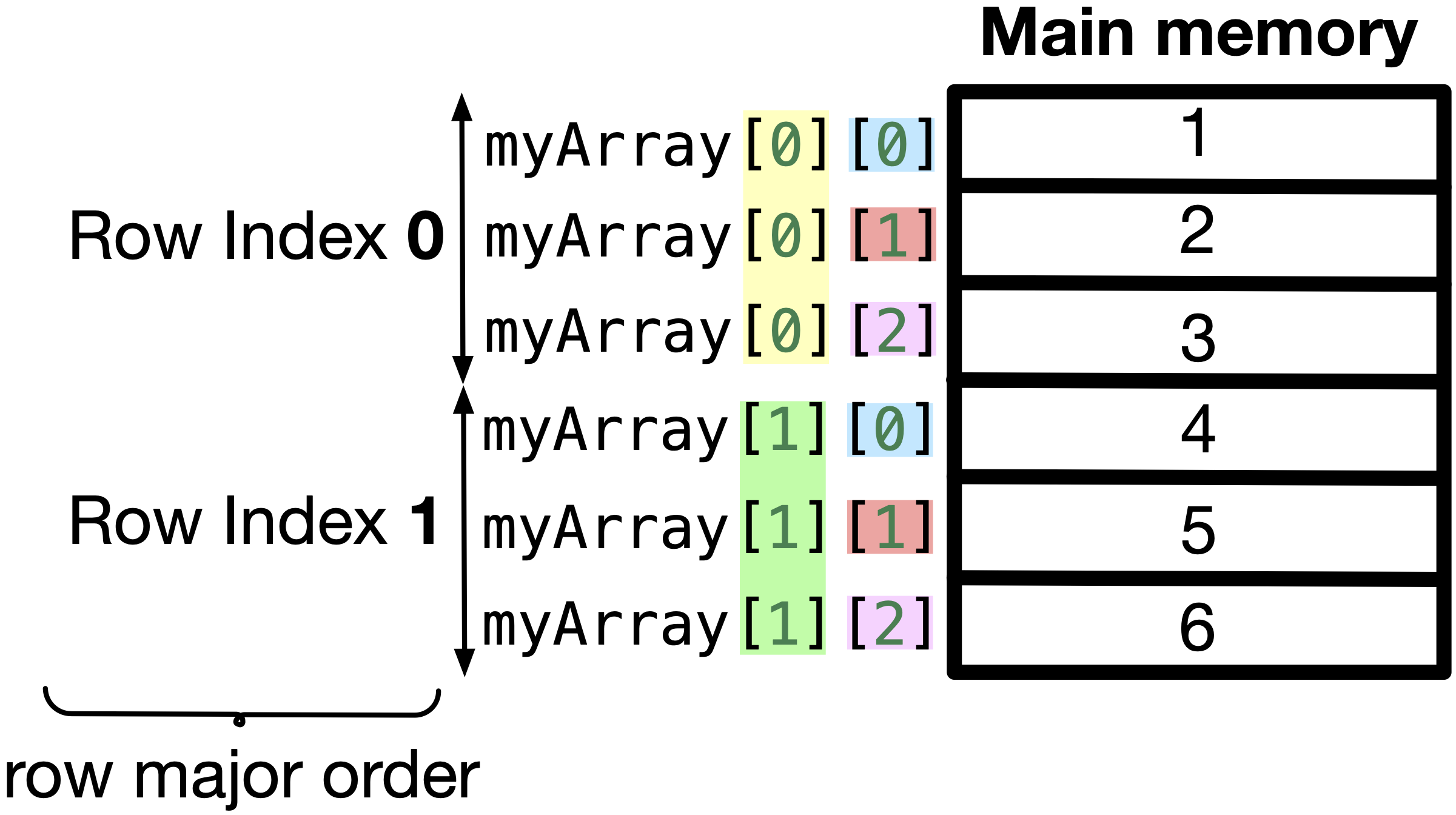
Fig. 9.3 Elements of a 2D array are stored in the memory sequentially row by row. This way of representing the elements of a multi-dimensional array is called row major order.#
&myArray[0][0] is the address of the first element of the array. The address of myArray[1][2] requires that we add to &myArray[0][0] \(((1 \times 3) + 2) \times\) sizeof(int), where \((1 \times 3)\) is to get to the second row, adding \(2\) is to get to the third column in the second row, and sizeof(int) is to multiply each step by the size of each int element. Generally, &myArray[i][j] is also &myArray[0][0] + (i * number of columns + j) * sizeof(int). The remaining addresses of the remaining elements are shown in Fig. 9.4.

Fig. 9.4 Addresses of the elements in a 2D array.#
Array identifier in 2D array
The array identifier of a 2D array is an alias for the address of the first element in the array, which is myArray[0][0], like 1D arrays. We also discuss this in the next section, when we pass a 2D array to a function.
Different from 1D arrays, the array identifier is also a pointer to the first row of the array. This can be confusing when you dereference a pointer to a 2D array (or array identifier), since it gives you a pointer to the first element of the first row of the array. For example, myArray holds the same value as *myArray, which is the address of myArray[0][0], i.e. myArray \(\Longleftrightarrow\) *myArray \(\Longleftrightarrow\) &myArray[0][0].
If you would add 1 to the 2D array identifier, this gives a pointer to the first element of the second row, for example, *(myArray + 1) is same as myArray[row].
Then, to get to a particular column, you need to add the index of the column. For example, *(*(myArray + 1) + 2) is same as myArray[1][2]. The following figure illustrates how can you use the array identifier to access elements.
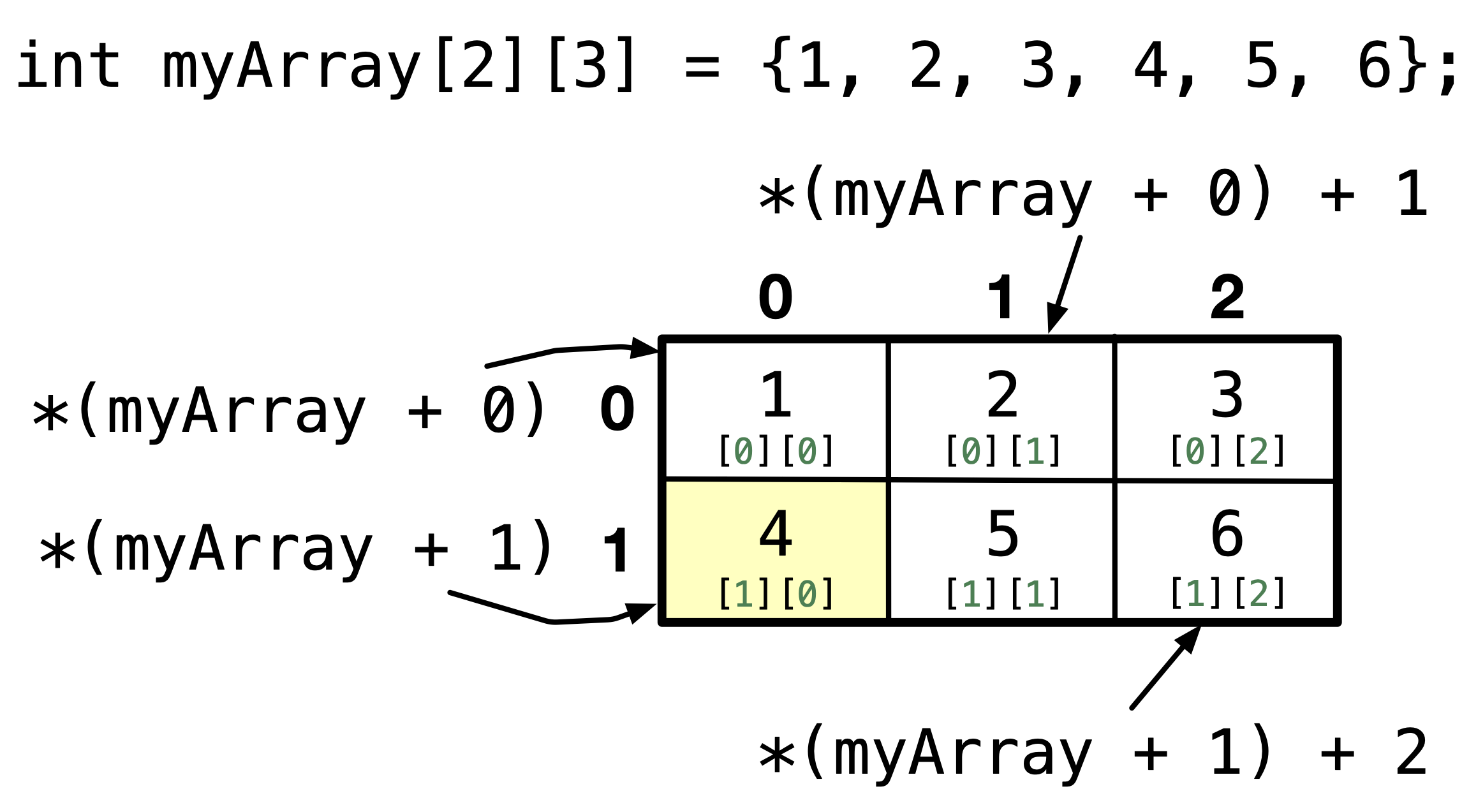
Code
#include <stdio.h>
int main(void) { int myArray[2][3];
for (int row = 0; row < 2; row++) { for (int col = 0; col < 3; col++) { myArray[row][col] = row * 3 + col + 1; } }
for (int row = 0; row < 2; row++) { for (int col = 0; col < 3; col++) { printf("%4d", *(*(myArray + row) + col)); // or printf("%4d", myArray[row][col]); } printf("\n"); }
return 0; }
9.1.3. Exercise#
Write a program that finds three horizontal consecutive \(1\)s in a \(6\) by \(6\) array.
Step 1: Toy example. In Fig. 9.5, we show a toy example of a \(6 \times 6\) array filled with \(0\)s and \(1\)s. We are required to find out that row, col \(= 2, 1\), and \(3, 2\) and \(5, 0\) have a \(1\) that is the beginning of \(3\) horizontal consecutive \(1\)s on the right.
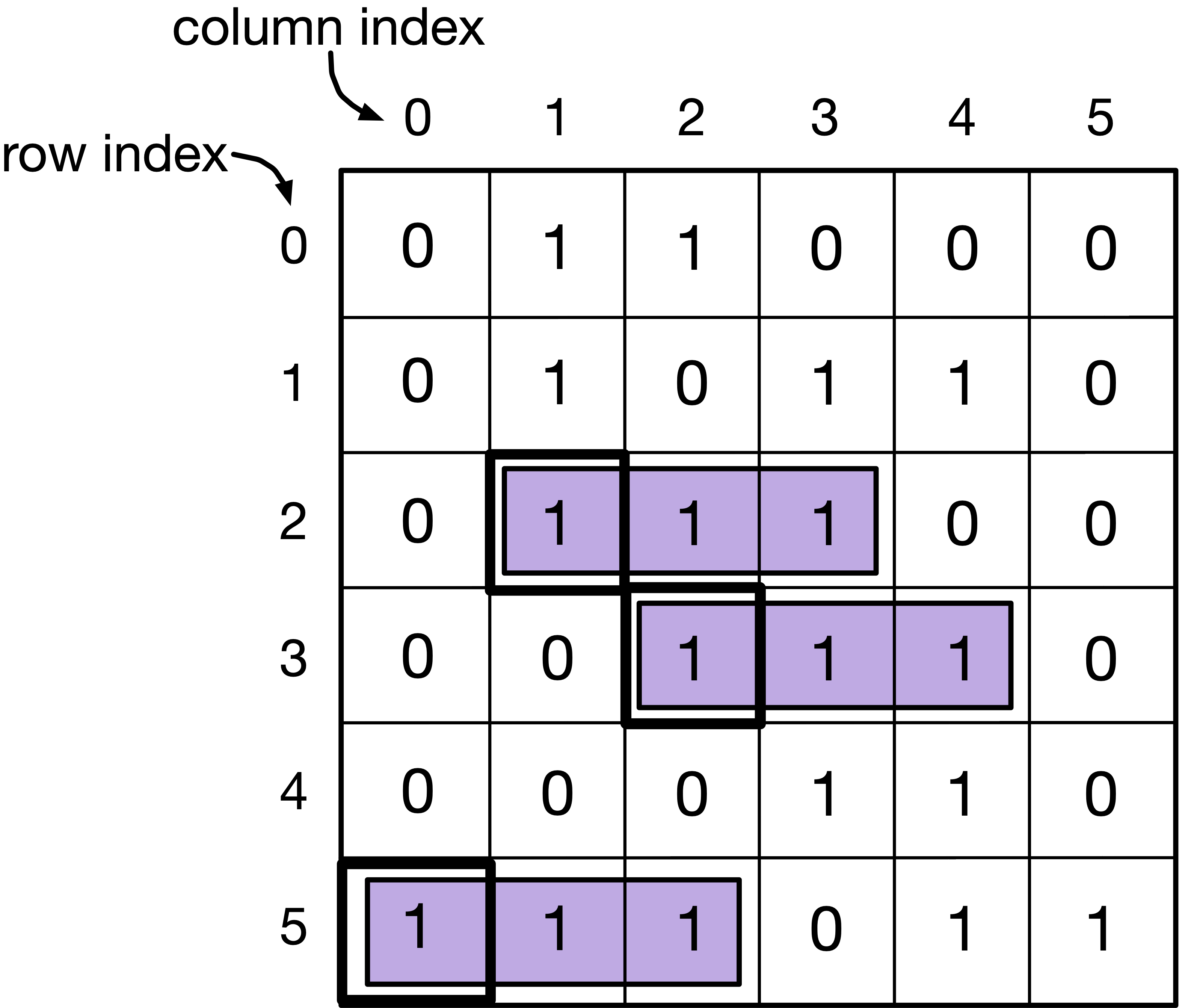
Fig. 9.5 \(6 \times 6\) array filled with \(0\)s and \(1\)s. You are required to print the starting row and column indices at which there are two other consecutive 1s on the right.#
Step 2: Think of a solution! We should loop over each element row by row in the 2D array from left to right. For each element, we will count how many \(1\)s we find in the current and the next two elements on the right. If the count is \(3\), we should print the row and column indices at which we found the consecutive horizontal line of \(1\)s.
Step 3: Decompose into steps. Given the \(6 \times 6\) array is in an array named board.
Set
row = 0andcol = 0Set
step = 0Set
count = 0If
board[row][col + step] == 1, increment count by \(1\)Increment
stepby \(1\) to go to the next element on the next columnRepeat \(4\) – \(5\) till step is \(3\) or if
col + step >= 6If
count == 3, printrowandcolGo to next element, and repeat \(2\) – \(7\) till
row = 6andcol = 6
Step 4: Write code. Download initialize-2d.c if you want to run the program yourself.
Code
#include <stdio.h>
int main(void) { int board[6][6] = { {0, 1, 1, 0, 0, 0}, {0, 1, 0, 1, 1, 0}, {0, 1, 1, 1, 0, 0}, {0, 0, 1, 1, 1, 0}, {0, 0, 0, 1, 1, 0}, {1, 1, 1, 0, 1, 1}, };
for (int row = 0; row < 6; row++) { for (int col = 0; col < 6; col++) { int count = 0; for (int step = 0; step < 3 && col + step < 6; step++) { if (board[row][col + step] == 1) { count += 1; } } if (count == 3) { printf("(row, col) = (%d, %d)\n", row, col); } } } return 0; }
Step 5: Test and debug your code. You can test your code with different array with different positions of the consecutive \(1\)s. A common mistake is to forget to check that col + step is without the bounds of the array. If you don’t, you will be accessing an element outside the bounds of the array, which might raise a “Segmentation Fault” error, because you are not permitted to access this location. Another common mistake is to forget to reset the count to \(0\) for each element. This will result in counting all the 1’s observed while looping over all rows and columns.
Quiz
0 Questions
